目录

 一、不用加号的加法

（1）原题再现

（2）问题分析

（3）完整代码

 二、走方格的方案数

（1）原题再现

（2）问题分析

（3）完整代码

 一、不用加号的加法

（1）原题再现

面试题 17.01. 不用加号的加法

        设计一个函数把两个数字相加。不得使用 + 或者其他算术运算符。

示例:

输入: a = 1, b = 1

输出: 2

（2）问题分析

        这道题要求不能用“+”等算数运算符，所以我们可以想到使用位运算符。

符号	描述	运算规则
&	与	两个位都为1时，结果才为1。
|	或	两个位都为0时，结果才为0。
^	异或	两个位相同为0，相异为1。
~	取反	0变1，1变0。
<<	左移	各二进位全部左移若干位，高位丢弃，低位补0
>>	右移	各二进位全部右移若干位，对无符号数，高位补0，有符号数，右移补1。

        本题可以使用&和^运算符，使用&得到两数相加的进位情况，使用^得到两数相加的结果（没有加进位）

（3）完整代码

class Solution {public int add(int a, int b) {// write code hereint ans=a^b;//无进位的情况下int carry=a&b;//需要进位的地方while(carry!=0) {carry=carry<<1;int tmp=ans;ans=ans^carry;carry=tmp&carry;}return ans;}
}

 二、走方格的方案数

（1）原题再现

走方格的方案数_牛客题霸_牛客网

描述

        请计算n*m的棋盘格子（n为横向的格子数，m为竖向的格子数）从棋盘左上角出发沿着边缘线从左上角走到右下角，总共有多少种走法，要求不能走回头路，即：只能往右和往下走，不能往左和往上走。

注：沿棋盘格之间的边缘线行走

输入描述：

输入两个正整数n和m，用空格隔开。(1≤n,m≤8)

输出描述：

输出一行结果

示例:

输入：

2 2

输出：

6

（2）问题分析

        这道题很明显是一道动态规划的题。需要额外注意的是n、m表示的是格子数，而我们走的是边，所以n和m都要+1，即2*2的4个格子有3*3的边框。

我们用二维数据记录每一步的状态。

状态：
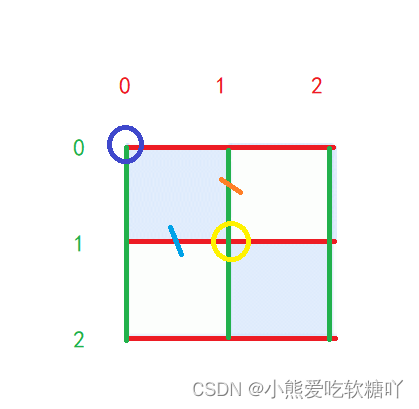
子状态：从(0,0)到达(1,0),(1,1),(2,1),...(n,m)的路径数
              F(i,j): 从(0,0)到达F(i,j)的路径数

        到达黄色这一状态时可能是从上面走下来，也可能是从左边走过来的。这一点的路径数，就是左边一点的路径数+上边一点的路径数。
状态递推：
              F(i,j) = F(i-1,j) + F(i,j-1)
初始化： 因为只能向左或者向下，所以当只有一行时，只能向左，走法也只有一种；同理，当只有一列时，只能向下，走法也只有一种。
              特殊情况：第0行和第0列
              F(0,i) = 1
              F(i,0) = 1
返回结果：右下角
              F(n,m)

（3）完整代码

import java.util.*;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();int m=sc.nextInt();int [][]maxNum=new int[n+1][m+1];for(int i=0;i<=m;i++) {maxNum[0][i]=1;}for(int i=0;i<=n;i++) {maxNum[i][0]=1;}for(int i=1;i<=n;i++) {for(int j=1;j<=m;j++) {maxNum[i][j]=maxNum[i-1][j]+maxNum[i][j-1];}}System.out.println(maxNum[n][m]);}
}

​

​