目录

问题描述：

计算最优值：

计算矩阵连乘积的动态规划算法： 

计算矩阵连乘积最优解的递归算法：

 输出最优次序：

问题描述：

m×n矩阵A与n×p矩阵B相乘需耗费的时间。
方法分析：
我们把mnp作为两个矩阵相乘所需时间的测量值。
现在假定要计算三个矩阵A、B和C的乘积，有两种方式计算此乘积。

先用A乘以B得到矩阵D，然后D乘以C得到最终结果，这种乘法的顺序为（AB）C；
另一种乘法的顺序为A（BC）。
尽管这两种不同的计算顺序所得的结果相同，但时间消耗会有很大的差距。
 

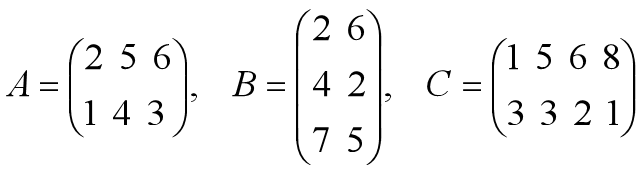
 因为矩阵乘法符合结合律，所以在计算ABC时，有两种方案，即(AB)C和A(BC)。

• 对于第一方案(AB)C，计算：

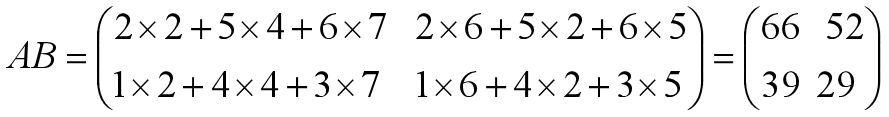
其乘法运算次数为：2×3 ×2=12

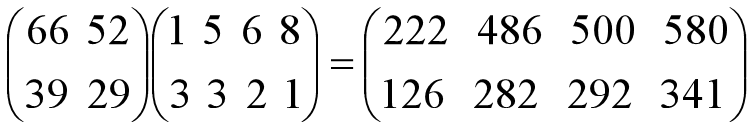
其乘法运算次数为：2×2×4=16。
总计算量为：12+16=28

• 对第二方案 A(BC)，计算： 

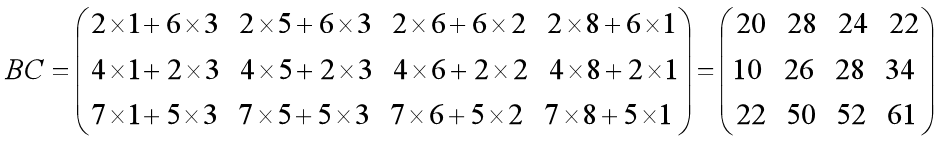
其乘法运算次数为：3×2×4=24

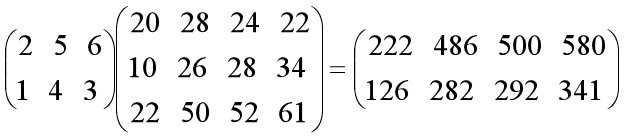
其乘法运算次数为：2×3×4=24。
总计算量为：24+24=48
可见，不同方案的乘法运算量，计算次数可能相差很悬殊。 

定义：
给定n个矩阵{A1,A2,…,An}，其中Ai与Ai+1是可乘的，i=1,2,…n-1。考察这n个矩阵的连乘积A1A2…An。

• 由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序。
• 这种计算次序可以用加括号的方式来确定。
• 若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积

完全加括号的矩阵连乘积可递归地定义为：
单个矩阵是完全加括号的；
矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，即A=(BC) 

• 设有四个矩阵A, B, C, D，总共有五种完全加括号的方式:

(A((BC)D))
(A(B(CD)))
((AB)(CD))
(((AB)C)D)
((A(BC)D))

具体实例：
设有四个矩阵A, B, C, D，它们的维数分别是：
A=50×10, B=10×40, C=40×30, D=30×5
矩阵A和B可乘的条件： 矩阵A的列数等于矩阵B的行数。
设A是p×q的矩阵, B是q×r的矩阵, 乘积是p×r的矩阵;计算量是pqr。
上述5种完全加括号方式的计算工作量为:
(A((BC)D)), (A(B(CD))), ((AB)(CD)), (((AB)C)D), ((A(BC)D))
16000, 10500, 36000, 87500, 34500
BC: 10×40×30 = 12000,
(BC)D: 10×30×5 = 1500,
(A((BC)D)): 50×10×5 = 2500
穷举法：
给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少？
穷举法：列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一种数乘次数最少的计算次序。
算法复杂度分析：
对于n个矩阵的连乘积，设其不同的计算次序为P(n)。
由于每种加括号方式都可以分解为两个子矩阵的加括号问题：(A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下：

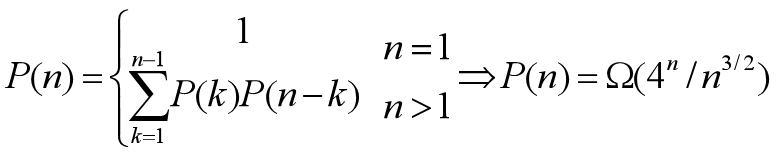
分析最优解的结构：

• 将矩阵连乘积AiAi+1…Aj 简记为A[i:j], 这里i≤j;
• 考察计算A[1:n]的最优计算次序。
• 设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，1≤k
• 计算量：A[1:k]的计算量加上A[k+1:n]的计算量，再加上A[1:k]和A[k+1:n]相乘的计算量。

特征：

• 计算A[1:n]的最优次序所包含的计算矩阵子链 A[1:k]和A[k+1:n]的次序也是最优的。
• 矩阵连乘计算次序问题的最优解包含着其子问题的最优解。
• 这种性质称为最优子结构性质。
• 问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。

建立递归关系：

• 设计算A[i: j]，1≤i≤j≤n，所需要的最少数乘次数m[i, j]，则原问题的最优值为m[1,n]
• 当i=j时，A[i: j]=Ai，因此，m[i, i]=0，i=1,2,…,n
• 当i

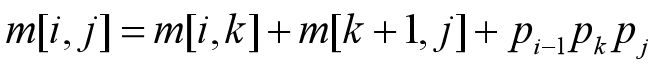
• 这里Ai的维数是Pi-1×Pi
• 

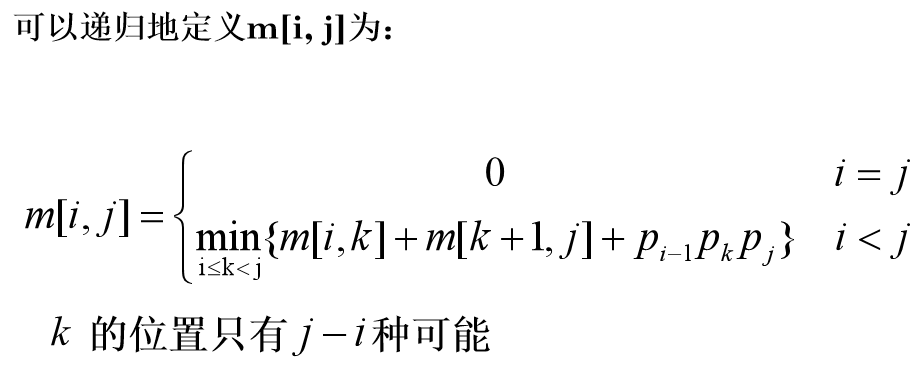
m[i][j]给出了最优值，最优断开位置为k： 

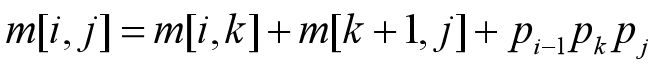
若将对应于m[i, j]的断开位置k记为s[i, j]，在计算出最优值m[i, j]后，可递归的由s[i, j]构造出相应的最优解。

计算最优值：

• 对于1≤i≤j≤n不同的有序对(i, j)对应于不同的子问题。因此，不同子问题的个数最多只有
• 

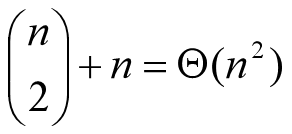
• 在递归计算时，许多子问题被重复计算多次。
• 这也是该问题可用动态规划算法求解的又一显著特征。
• 用动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算。
• 在计算过程中，保存已解决的子问题答案。
• 每个子问题只计算一次，在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法。

计算矩阵连乘积的动态规划算法： 

void MatrixChain(int n) {for (int i = 1; i <= n; i++)m[i][i] = 0;for(int r=2;r<=n;r++)for (int i = 1; i <= n - r + 1;i++) {int j = i + r - 1;//计算初值，从i出断开m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];s[i][j] = i;//记录断开位置for (int k = i + 1; k < j; k++) {  //k处断开int t;t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];if (t < m[i][j]) {m[i][j] = t;s[i][j] = k;}}}
}

计算矩阵连乘积最优解的递归算法：

//计算矩阵连乘积最优解的递归算法
void TraceBcak(int i,int j) {if (i == j)cout <<"A"<< i<<" ";else{cout << "(";TraceBcak(i, s[i][j]);TraceBcak(s[i][j] + 1, j);cout << ")";}
}

 输出最优次序：

/*
* 计算矩阵连乘积的动态规划算法
*/#include
using namespace std;
const int NUM = 51;
int p[NUM];
int m[NUM][NUM];
int s[NUM][NUM];
void MatrixChain(int n) {for (int i = 1; i <= n; i++)m[i][i] = 0;for(int r=2;r<=n;r++)for (int i = 1; i <= n - r + 1;i++) {int j = i + r - 1;//计算初值，从i出断开m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];s[i][j] = i;//记录断开位置for (int k = i + 1; k < j; k++) {  //k处断开int t;t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];if (t < m[i][j]) {m[i][j] = t;s[i][j] = k;}}}
}//计算矩阵连乘积最优解的递归算法
void TraceBcak(int i,int j) {if (i == j)cout <<"A"<< i<<" ";else{cout << "(";TraceBcak(i, s[i][j]);TraceBcak(s[i][j] + 1, j);cout << ")";}
}int main() {int p[] = { 10, 100, 5, 50 };int n = sizeof(p) / sizeof(p[0]);MatrixChain(n);TraceBcak(1, n);return 0;
}