[图神经网络]图特征工程
一、图的特征
图点本身就具备的特征称为属性特征(如:连接权重、节点类型等),属性特征大部分时候都是多模态的。
图中一个节点和其他节点之间的连接关系称为连接特征(结构信息)
人工提取并构造的特征称为特征工程。(将图变为向量)特征工程一般针对图的连接特征进行构造
二、节点层面的特征工程
一般而言,节点层面连接特征分为:
①节点的连接数
②节点的重要度
③节点的聚集系数(某节点与其相邻节点之间是否有联系)
④节点的子图信息(某节点周围有多少人工定义的子图)
1.节点连接数
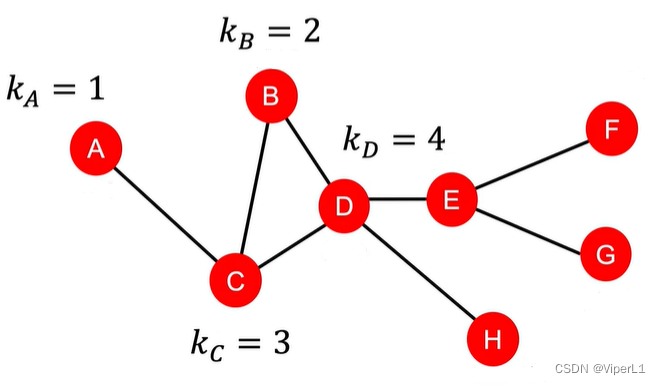
若求节点连接数,直接按某行/某列求和即可;或将邻接矩阵与一个值为1的向量相乘即可。但节点连接数不考虑连接的质量,所以引入下面三个指标来衡量节点连接的质量。
2.节点重要度
①特征向量重要度(Eigenvector Centrality)
某节点的重要度=与其相邻节点的重要度之和,公式表示为:
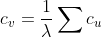 其中
其中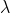 仅用于归一化
仅用于归一化
因为其是一个递归算法,实际计算转换为求邻接矩阵A矩阵的特征向量的问题
 其中c为邻接矩阵A的特征向量(由与该节点相连的所有节点的重要度组成);邻接矩阵A用以表示这些节点的连接属性;
其中c为邻接矩阵A的特征向量(由与该节点相连的所有节点的重要度组成);邻接矩阵A用以表示这些节点的连接属性;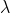 即为目标节点的重要度。
即为目标节点的重要度。
②介数重要度(Betweennness Centrality)
用以衡量一个节点是否处在交通咽喉处;计算方法为:对连通域中除了要求的节点外的所有节点,求其最短距离中有多少个必须经过该节点。如下图:
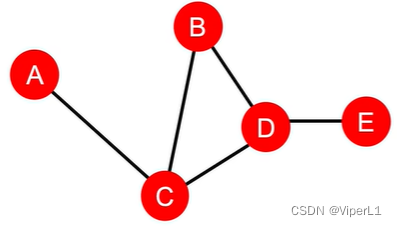
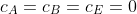 ,而
,而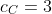 (路径为:A-C-B、A-C-D、A-C-D-E)
(路径为:A-C-B、A-C-D、A-C-D-E)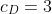
3.集群系数(Clustering Coefficient)
计算方法为:该节点的周围节点之间相连数 / 该节点与周围节点相连数,值域为[0,1]...(简单点理解就是三角形的个数)。详见下图示例:

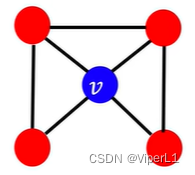
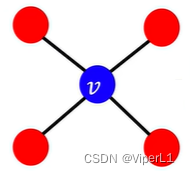
计算结果分别为: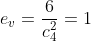 、
、、

这种三角形连接被称为:自我中心网络(ego-network)
4.graphlet
相同样的节点数构成非同形子图(类似同分异构体),例如4个节点可以构成6种graphlet。
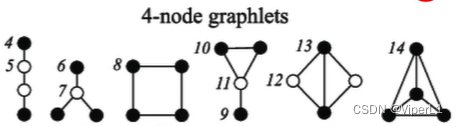
提取某节点周围的graphlet个数即可构成一个称为Graphlet Degree Vector(GDV),如下图所示:
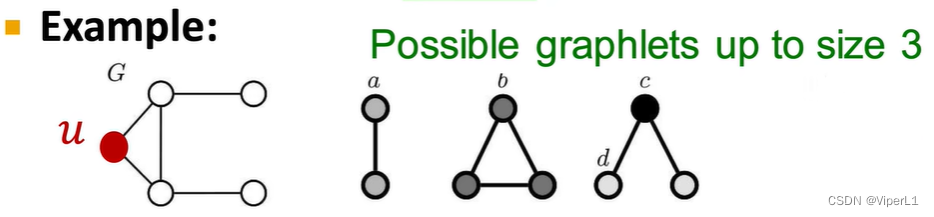
节点u可能出现的子图形式有三种,分别列出含有u节点的子图类型
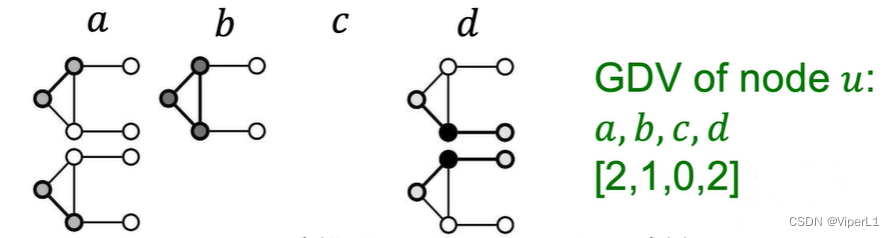
GDV可以描述节点u的局部邻域拓扑结构信息。
三、连接层面的特征工程
目的:通过已知连接补齐未知连接。可以通过两种方法来获取D维向量:
①直接提取连接的特征
②将连接两端节点的D维向量拼在一起(但这种方法会丢失link本身的连接信息)
连接预测的一般方法为:
①获取连接的D维向量
②将D维向量送入机器学习中进行计算,获得分数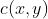
③将分数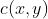 进行排序,选出最高的n个新连接
进行排序,选出最高的n个新连接
④计算这n个预测结果与真实值
1.连接特征
连接特征一般分为:①节点间的距离;②节点局部连接信息;③节点在全图的连接信息
①最短路径长度
即两个点之间经过节点最少的路径上的节点数,但是其与节点连接数一样只看数量不看权重。
②基于两节点的局部连接信息
共同相邻节点个数;交并比等。但若两个节点不存在局部连接,则其交并比和共同相邻节点个数均会为0。例如下图中A和E就不存局部连接。
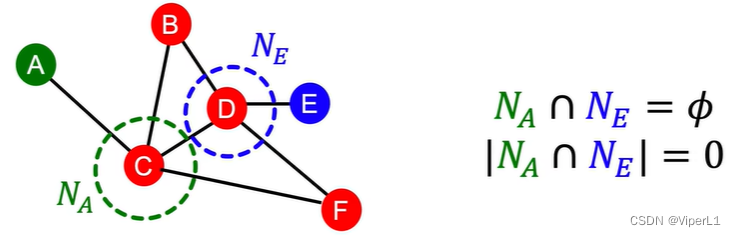
③卡兹系数(Katz index)
表示节点u和节点v之间的长度为k的路径个数。计算方法:使用邻接矩阵的幂来计算,如下:
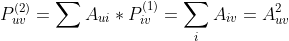
此式的实际意义为: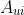 =与u隔1步的邻居i;
=与u隔1步的邻居i;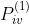 =i是否与v隔1步
=i是否与v隔1步

由数学归纳法可知:长度为 的矩阵为
 (矩阵
(矩阵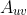 的
的 次方中第u行第v列的元素)
卡兹系数公式可以通过矩阵几何级数化简为:
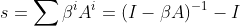 其中
其中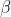 为折减系数,位于0到1之间;
为折减系数,位于0到1之间;为单位矩阵。
四、全图层面的特征工程
目的是提取整张图的特征,将其变为D维向量,反映全图结构特点。
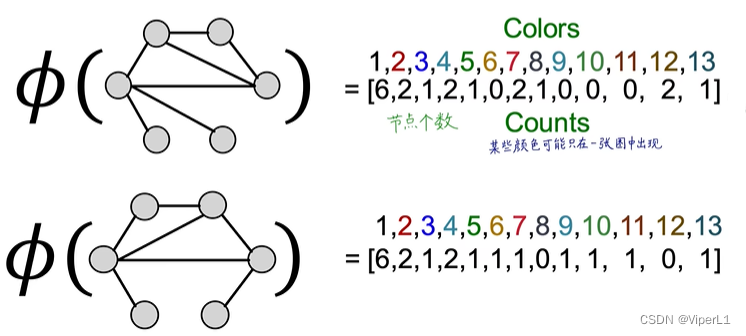
实际就是在计算不同特征在图中存在的个数(将图视为文章,节点视为单词--Bag-of-Nodes)
但这种方法有一个缺陷,就是只看是否存在第 i 个节点而不关心连接结构,如下图中两个图编码的D维向量一致,均为[1 1 1 1]
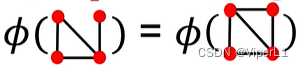
还可以使用Bag-of-Node-degrees,但是同样的只看node dgree,不看节点也不看连接结构
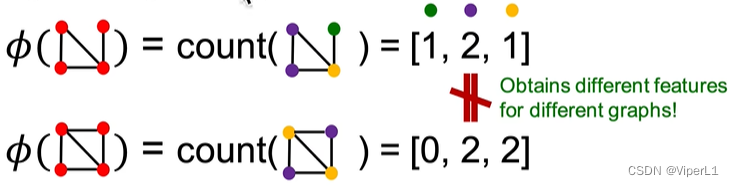
Bag-of-xxx可以推广到之前提到的任意特征中,比如将全图的graphlets作为应用场景,其相较于节点层面的graphlets有如下区别:①可以存在孤立节点;②计数对象为全图,而不是特定节点邻域。

将两张图的graphlet进行数量积则可得到Graphlet Kernel(一个标量),该指标可以反映两张图是否相近/匹配,公式记作:
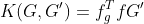
若两张图尺寸不一致则需要对其进行归一化
但是这种做法对算力的消耗极大。故一般采用Weisfeiler-Lehman Kernel算法,采用的是颜色微调的思想(Color refinement),其具体做法如下:
①将图初始化一个有一个编码
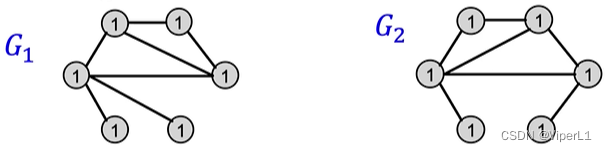
②根据具体节点的连接数量,对其编码进行调整
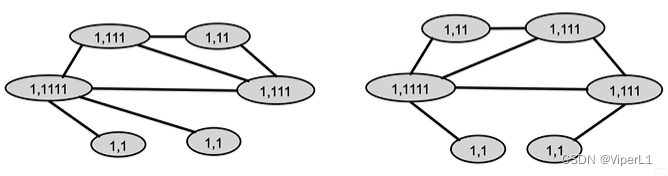
③将不同的编码以不同的颜色代替(Hash)


以上步骤可以重复进行,最后两个相同结构的节点颜色始终相同
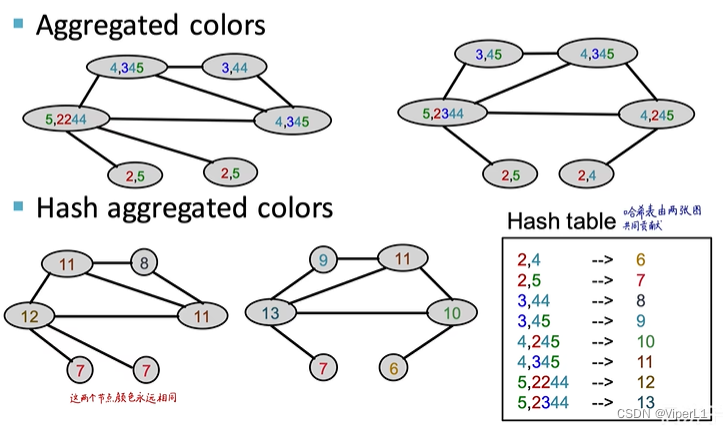
这样就将每张图变成了一个维度较低的向量。将这两张图的向量求内积即可得到Weisfeiler-Lehman kernel
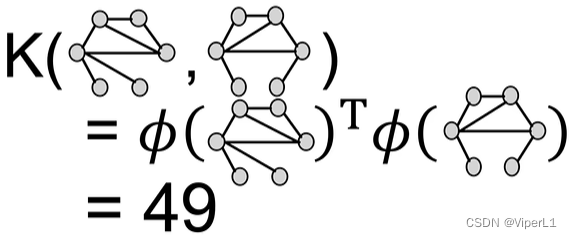
上述操作可以记作: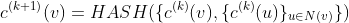 , k 表示上述编码过程进行了 k 步,表示捕获了图中 k 跳个连接
, k 表示上述编码过程进行了 k 步,表示捕获了图中 k 跳个连接
