文章目录

• • • 一、Auto-Encoders简介
    • 二、变种AE介绍
    • • Denoising AutoEncoders
      • Dropout AutoEncoders
      • Adversarial AutoEncoders
      • Varational Auto Encoder
    • 三、Auto-Encoders实战
    • • Auto-Encoders
      • Varational Auto Encoder

一、Auto-Encoders简介

自编码器（AE）是一类用于半监督、无监督学习中的神经网络，对输入信息x学习从而生成一个类似数据。输入和学习目标相同，结构分为编码器和解码器两部分，形象图如下：

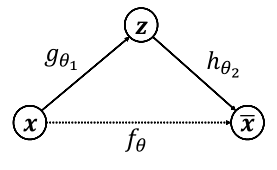
• gθ1g\theta_1gθ1​和hθ2h\theta_2hθ2​分别表示编码网络（高维到低维）和解码网络（低维到高维）
• fθf_\thetafθ​表示希望学习到的映射
• 优化目标：Minimizer=dist(x,xˉ)Minimizer=dist(x,\bar x)Minimizer=dist(x,xˉ)，dist(x,x)dist(x,x)dist(x,x)表示重建误差函数

自动编码器主要是一种降维（或压缩）算法，具有以下几个重要特性：

• 特定的数据：只能有意义压缩训练过的或与训练时相似的数据
• 有损：输入和输出不完全相同，不可能无损压缩
• 无监督：输入原始数据并自我监督（所以又叫自我监督）

PCA V.S. Auto-Encoders

• PCA仅限于线性映射，在高维数据中它只选择具有最大方差的样本。线性传递函数的单层自动编码器可以等价于PCA
• 如果AE中不使用线性函数，AE相对PCA可能找到不同的子空间

二、变种AE介绍

尝试学习数据的真实分布

Denoising AutoEncoders

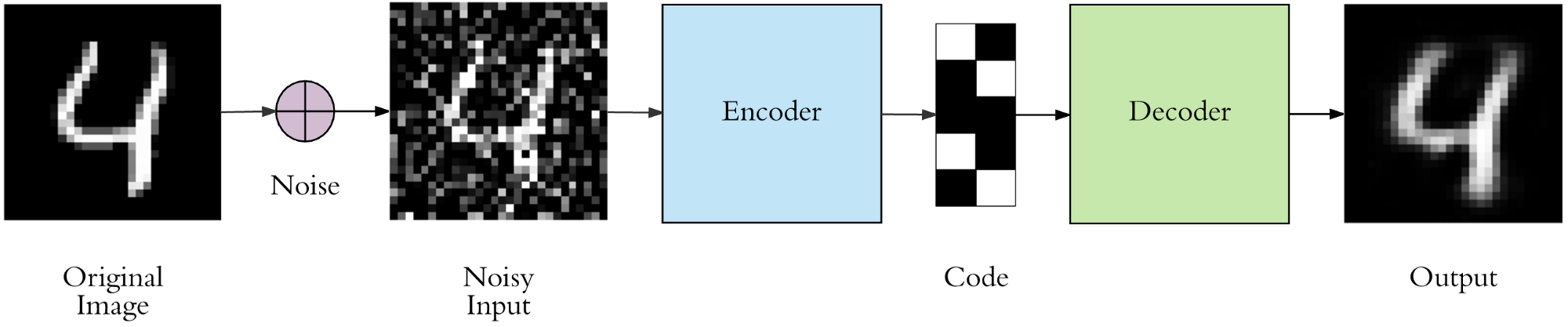
AE得到的初始模型往往具有过拟合的风险，为了防止输入数据的底层特征而添加随机的噪声干扰，使得到的结果具有较强的鲁棒性，增强泛化能力

Dropout AutoEncoders

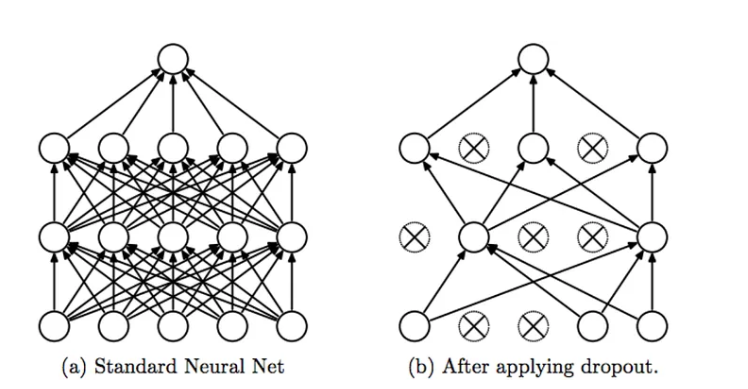
神经网络中常用的技巧，即以某个概率随机断掉部分连接层，减少过拟合的程度

Adversarial AutoEncoders

仿照GAN的训练方式来训练自编码器网络，通过变分推理先验确保从先验空间的任何部分生成有意义的样本。自编码器训练有了第二个目标-对抗性训练准则，使自编码器不仅能够重建还能服从某个分布

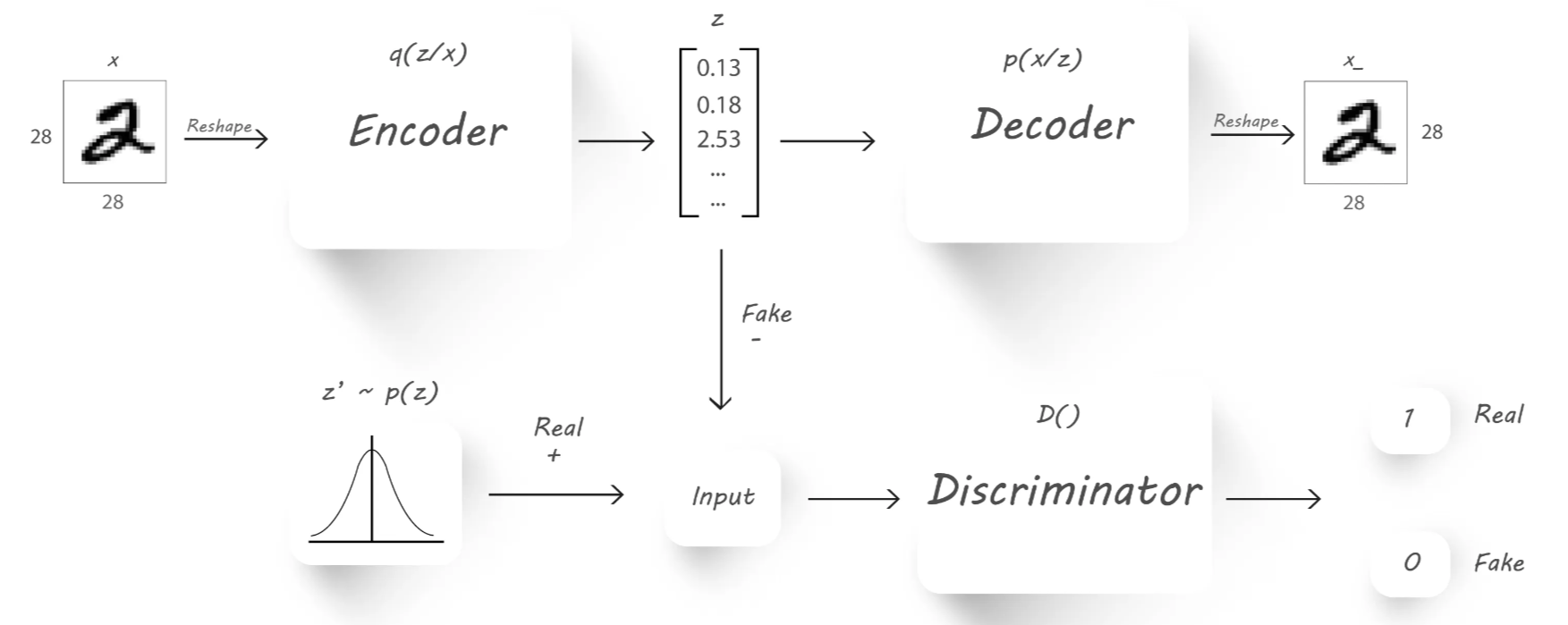
相关链接

Varational Auto Encoder

编码过程中增加限制，使生成的隐含向量能服从单位高斯分布，这样只需要向解码器提供从单位高斯分布的采样就可以生成新的数据。通过KL divergence来衡量不同分布的相似程度，公式如下：
DKL(P∣∣Q)=∫−∞∞p(x)logp(x)q(x)dxDKL(P||Q)= \int_{-\infty }^{\infty }p(x)log\frac{p(x)}{q(x)}dxDKL(P∣∣Q)=∫−∞∞​p(x)logq(x)p(x)​dx
和AE中的目标一起做loss，让网络自己权衡即可

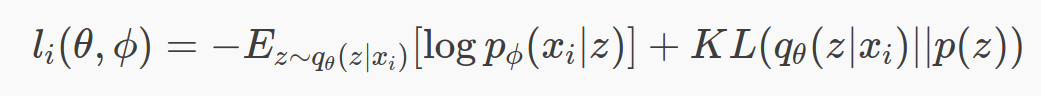
三、Auto-Encoders实战

Auto-Encoders

ae.py

from torch import nnclass AE(nn.Module):def __init__(self):super(AE,self).__init__()self.encoder = nn.Sequential(nn.Linear(784,256),nn.ReLU(),nn.Linear(256,64),nn.ReLU(),nn.Linear(64,20),nn.ReLU())self.decoder = nn.Sequential(nn.Linear(20,64),nn.ReLU(),nn.Linear(64,256),nn.ReLU(),nn.Linear(256,784),nn.Sigmoid())def forward(self,x):# x:[b,1,28,28]batchsz = x.size(0)x = x.view(batchsz,784)x = self.encoder(x)x = self.decoder(x)x = x.view(batchsz,1,28,28)return x,None

main.py

import torch
from torch.utils.data import DataLoader
from torchvision import transforms,datasets
from ae import AE
from torch import nn,optim
import visdomdef main():mnist_train = datasets.MNIST('mnist',True,transform=transforms.Compose([transforms.ToTensor()]),download=True)mnist_train = DataLoader(mnist_train,batch_size=32,shuffle=True)mnist_test = datasets.MNIST('mnist',False,transform=transforms.Compose([transforms.ToTensor()]),download=True)mnist_test = DataLoader(mnist_test,batch_size=32,shuffle=True)x, _ = iter(mnist_train).next()print('x',x.shape)device = torch.device('cuda')model = AE().to(device)criteon = nn.MSELoss()optimizer = optim.Adam(model.parameters(),lr=1e-3)print(model)viz = visdom.Visdom()for epoch in range(1000):for batchidx, (x,_) in enumerate(mnist_train):# [b,1, 28, 28]x = x.to(device)x_hat,_ = model(x)loss = criteon(x_hat,x)#backpropoptimizer.zero_grad()loss.backward()optimizer.step()print(epoch,'loss:',loss.item())x,_ = iter(mnist_test).next()x = x.to(device)with torch.no_grad():x_hat,_ = model(x)viz.images(x,nrow=8,win='x',opts=dict(title='x'))viz.images(x_hat,nrow=8,win='x_hat',opts=dict(title='x_hat'))if __name__ == '__main__':main()

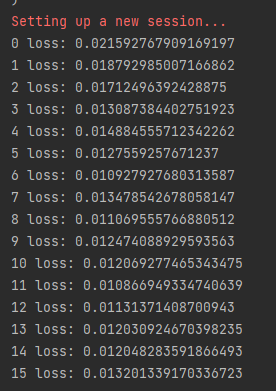
训练第一次表现：

迭代训练15次后表现：

Varational Auto Encoder

main.py

import torch
from torch.utils.data import DataLoader
from torchvision import transforms,datasets
from vae import VAE
from torch import nn,optim
import visdomdef main():mnist_train = datasets.MNIST('mnist',True,transform=transforms.Compose([transforms.ToTensor()]),download=True)mnist_train = DataLoader(mnist_train,batch_size=32,shuffle=True)mnist_test = datasets.MNIST('mnist',False,transform=transforms.Compose([transforms.ToTensor()]),download=True)mnist_test = DataLoader(mnist_test,batch_size=32,shuffle=True)x, _ = iter(mnist_train).next()print('x',x.shape)device = torch.device('cuda')model = VAE().to(device)criteon = nn.MSELoss()optimizer = optim.Adam(model.parameters(),lr=1e-3)print(model)viz = visdom.Visdom()for epoch in range(1000):for batchidx, (x,_) in enumerate(mnist_train):# [b,1, 28, 28]x = x.to(device)x_hat,kld = model(x)loss = criteon(x_hat,x)if kld is not None:elbo = -loss - 1.0* kldloss = -elbo#backpropoptimizer.zero_grad()loss.backward()optimizer.step()print(epoch,'loss:',loss.item(),'kld:',kld.item())x,_ = iter(mnist_test).next()x = x.to(device)with torch.no_grad():x_hat,kld = model(x)viz.images(x,nrow=8,win='x',opts=dict(title='x'))viz.images(x_hat,nrow=8,win='x_hat',opts=dict(title='x_hat'))if __name__ == '__main__':main()

vae.py

import torch
from torch import nnclass VAE(nn.Module):def __init__(self):super(VAE,self).__init__()# [b,784]=>[b.20]# u:[b,10]# Sigma: [b,10]self.encoder = nn.Sequential(nn.Linear(784,256),nn.ReLU(),nn.Linear(256,64),nn.ReLU(),nn.Linear(64,20),nn.ReLU())# [b,20] => [b,784]self.decoder = nn.Sequential(nn.Linear(10,64),nn.ReLU(),nn.Linear(64,256),nn.ReLU(),nn.Linear(256,784),nn.Sigmoid())def forward(self,x):# x:[b,1,28,28]batchsz = x.size(0)#flattenx = x.view(batchsz,784)# [b,20] ,including mean and sigmah_ = self.encoder(x)# [b,20] => [b,10] and [b,10]mu,sigma = h_.chunk(2,dim=1)# reparemetrize_trick: epison~N(0,1)h = mu + sigma * torch.randn_like(sigma)x_hat = self.decoder(h)x_hat = x_hat.view(batchsz,1,28,28)kid = 0.5 * torch.sum(torch.pow(mu,2)+torch.pow(sigma,2) -torch.log(1e-8+torch.pow(sigma,2))-1)/(batchsz*28*28)return x_hat,kid

训练第一次表现：

迭代训练15次后表现：

得到kld值计算过程如下：

kid = 0.5 * torch.sum(torch.pow(mu,2)+torch.pow(sigma,2) -torch.log(1e-8+torch.pow(sigma,2))-1
)

KL计算公式：

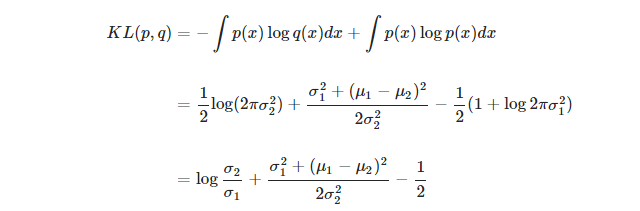
其中ppp,qqq在本次实验中分别表示单位高斯分布，和训练的N∼(μ,σ)N\sim (\mu,\sigma)N∼(μ,σ),代入上面计算化简即可