《括号序列》真题练习
写在前面的话： 真离谱，这题改了一天，现在还是没过
题目大意： 给你一个只含有’(‘和’)‘的字符串，你需要向这个字符串当中添加’(‘和’)'，以实现这个字符串的括号匹配。
动态规划的思路：我之前想了一个排列组合的方法，但是，emmm,太麻烦了b
设dp[i][j]dp[i][j]dp[i][j]的含义是向第iii个多出来的右括号前面插入jjj个左括号。并且我们把一个字符串按照多出来的右括号进行分区，比如说:(())∣)∣(())|)|(())∣)∣，然后考虑状态转移方程：dp[i][j]dp[i][j]dp[i][j]可以由dp[i−1][0]+dp[i−1][1]+...+dp[i−1][j]dp[i-1][0]+dp[i-1][1]+...+dp[i-1][j]dp[i−1][0]+dp[i−1][1]+...+dp[i−1][j]转移过来，比如说，在前i−1i-1i−1个区域里面已经插入了kkk个字符，那么在第iii个区域再插入j−kj-kj−k个字符即可。注意这第iii个区域一定是没有左括号的那个区域，否则这个区域的右括号就不是多出来的右括号。
先放个代码，明天再改吧。

#include
#include
#include
#include
using namespace std;
int mod = 1e9 + 7;
int dp[6000][6000];
int solve(char p[],int cnt)
{int sum[6000]; int tmp = cnt;sum[0] = (p[0] == '(' ? 1 : 0);if (p[0] == '(')tmp--;for (int i = 1; p[i] != '\0'; i++){//sum[i]=sum[i-1]+ (p[i] == '(' ? 1 : 0);if (p[i] == '('){sum[i] = sum[i - 1] + 1;tmp--;}elsesum[i] = sum[i - 1];}if (tmp < 0)return 1;if (tmp == 0)return 0;int pre[6000];int yh[6000];int s = 0;for (int i = 0; p[i] != '\0'; i++)if (p[i] == ')')yh[s++] = sum[i];for (int i = 1-yh[0]; i <= cnt; i++){dp[1][i] = 1;if (i <1)pre[i] = dp[1][i];elsepre[i] = pre[i - 1] + 1;}for (int i = 2; i <= cnt; i++){vector nxt(cnt + 5, 0);for (int j = max(i-yh[i-1],0); j <= tmp; j++){dp[i][j] = pre[j];if (j - 1 < 0)nxt[j] = dp[i][j];elsenxt[j] = nxt[j - 1] + dp[i][j];}for (int i = 1; i <= cnt; i++)pre[i] = nxt[i];}/*for (int i = 1; i <= cnt; i++){for (int j = 1; j <= cnt; j++){printf("%5d ", dp[i][j]);}printf("\n");}printf("\n\n***********%d", tmp);*/return dp[cnt][tmp];
}
char rev(char s)
{if (s == ')')return '(';elsereturn ')';
}
int main(void)
{char p[6000];scanf_s("%s", p, sizeof(p));//先看有几个右括号int cnt = 0;int len = 0;for (int i = 0; p[i] != '\0'; i++){if (p[i] == ')')cnt++;len++;}int a=solve(p, cnt);char s[6000];cnt = 0;for (int i = len - 1; i >= 0; i--){s[len - 1 - i] = rev(p[i]);if (s[len - 1 - i] == ')')cnt++;}s[len] = '\0';int b=solve(s, cnt);printf("%d", (long long)a*b%mod);
}

下一个题是线性基相关，前文在这里：点我
题目：E. The Tree Has Fallen!

过掉这个题的过程还是很心酸的
写完忘了及时更新博客giao，哦对了，我想起来为啥了，因为数据库3.3/4(懂得都懂）
题目大意： 首先给出一棵树，没有指定根，每一个节点都有一个编号和权值，现在给出若干查询，指定根rrr和节点vvv，求以rrr为根的树，以v为父节点/祖先的子树中的全部节点的权值异或和最大值为多少。
解题思路： 这个题我以为只考线性基，结果根本不是，每一次指定rrr和vvv的时候，我都去bfsbfsbfs一遍，当然不对。(TLETLETLE)
只要判断以1为根的节点的各个节点的线性基即可。这里还要分情况，一共有3种。

1. r==vr==vr==v
2. 当1为根的时候，r是v的祖先。
3. 当1为根的时候，v是r的祖先。

情况1是整个树的线性基去求。
情况2是1为根是v子树的线性基去求。
前两种情况证明略去。
情况3有点复杂

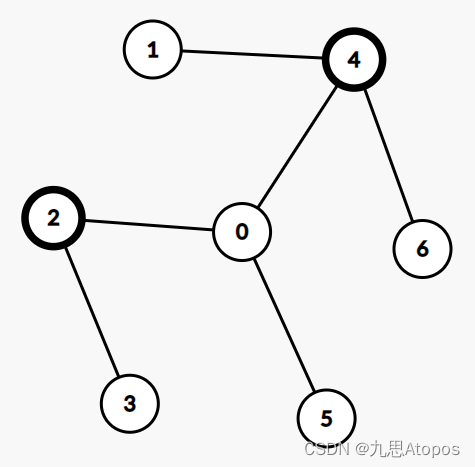
假设r是2，4是v，则线性基应该排除从2到4路径上的所有节点形成的子树（包括2），所以就涉及到了前缀线性基和后缀线性基。
这里的做法为：

pr是前缀线性基，bh为后缀线性基，ans是维护了一个刨除掉一个子树的整棵树的线性基，因为经过剖分之后，一个子树的序号是连续的，所以说1∼n1 \sim n1∼n的序号刨除掉i∼ji \sim ji∼j，结果就是1∼(i−1)1 \sim (i-1)1∼(i−1)和(j+1)∼n(j+1) \sim n(j+1)∼n， ‘ ~ ’左右为闭区间。
所以只需要找到低于4的一级，把这一级子树都刨除掉就可以，也就是ans[0]ans[0]ans[0]。
放一个画二叉树的链接。这里
代码：

#include
#include
#include
using namespace std;
const int length = 2e5 + 5;
int cost[length];
int cost_new[length];
int dfn[length];
int sz[length];
int lg[length];
vector> edge(length);
struct s mrg(struct s &a, struct s &b);
int lca(int r, int v);
void dfs_id(int cur, int fa);
//在dfs_id中算子树的线性基
//由于没有pos，所以算的时候实际上只用到了编号连续，好像和
//树链剖分没啥关系了
//lca用到剖分了吗？
int min(int a, int b)
{if (a < b)return a;else return b;
}
struct s
{int dp[32];void clear(){for (int i = 0; i < 32; i++)dp[i] = 0;}void ist(int x)//插入x这个数{int tmp = (int)(log(x)/log(2));tmp++;for (int i = 31; i >= 0; i--){if (!x)return;if (x&(1 << i)){if (dp[i] == 0){dp[i] = x; break;}x = dp[i] ^ x;}}}int qur(){int ans = 0;for (int i = 31; i >= 0; i--){if ((ans^dp[i]) > ans)ans = ans ^ dp[i];}return ans;}
};
struct s pr[length], bh[length];
//pr为从1到i的前缀线性基
//bh为从i到n的后缀线性基
struct s fm[length];
//fm表示以dfn[i]为根节点的线性基
int ans[length];
int ans_nom[length];
int vis[length];
int dep[length];
int son[length];
int father[length][20];
void dfs(int cur, int fa,int depth)
{dep[cur] = depth;int t = -1;int maxa = -1;for (int j : edge[cur]){if (vis[j] == 0&&j!=fa){vis[j] = 1;father[j][0] = cur;for (int i = 1; i < lg[depth+1]; i++){father[j][i] = father[father[j][i - 1]][i - 1];}dfs(j, cur,depth+1);if (maxa < sz[j]){t = j;maxa = sz[j];}sz[cur] += sz[j];vis[j] = 0;}}sz[cur]++;son[cur] = t;}
int cnt = 0;
void dfs_id(int cur, int fa)
{dfn[cur] = ++cnt;fm[cur].ist(cost[cur]);if (son[cur] != -1){dfs_id(son[cur], cur);fm[cur] = mrg(fm[cur], fm[son[cur]]);}for (int j : edge[cur]){if (vis[j] == 0 && j != fa&&j!=son[cur]){vis[j] = 1;dfs_id(j, cur);fm[cur] = mrg(fm[cur], fm[j]);vis[j] = 0;}}
}
int lca(int r, int v)
{int x, y;x = r;y = v;if (dep[x] < dep[y])swap(x, y);while (dep[x] > dep[y]){x = father[x][lg[dep[x] - dep[y]] - 1];}if (x == y)return x;for (int k = lg[dep[x]] - 1; k >= 0; k--){if (father[x][k] != father[y][k]){x = father[x][k];y = father[y][k];}}return father[x][0];
}
int lca_cal(int r, int v)
{while (dep[r] > dep[v] + 1){r = father[r][lg[dep[r] - dep[v] - 1] - 1];}return r;
}
//一个是前缀，一个是后缀
int solve(int r, int v)
{if (r == v){return ans_nom[1];}else if (lca(r, v) == v){return ans[lca_cal(r, v)];}else{return ans_nom[v];}
}struct s mrg(struct s &a, struct s &b)
{struct s tmp = a;for (int i = 31; i >= 0; i--){tmp.ist(b.dp[i]);}return tmp;
}
void clc(int i)
{edge[i].clear();pr[i].clear();bh[i].clear();fm[i].clear();dfn[i] = 0;sz[i] = 0;son[i] = 0;for (int j = 0; j < 20; j++)father[i][j] = 0;
}int main(void)
{int t;scanf_s("%d", &t);lg[0] = 1;for (int i = 0; i < length; i++){lg[i] = lg[i - 1] + ((i == (1 << lg[i - 1])) ? 1 : 0);}for (int i = 0; i < t; i++){int n;scanf_s("%d", &n);for (int i = 1; i <= n; i++){scanf_s("%d", &cost[i]);clc(i);}//for(int i=n+1;iint a, b;scanf_s("%d%d", &a, &b);edge[a].push_back(b);edge[b].push_back(a);}vis[1] = 1;dfs(1,-1,0);vis[1] = 1;dfs_id(1,-1);//处理标号for (int i = 1; i <= n; i++){cost_new[dfn[i]] = cost[i];}pr[1].ist(cost_new[1]);for (int i = 2; i <= n; i++){pr[i] = pr[i - 1];pr[i].ist(cost_new[i]);}bh[n].ist(cost_new[n]);for (int i = n - 1; i >= 1; i--){bh[i] = bh[i + 1];bh[i].ist(cost_new[i]);}for (int i = 1; i <= n; i++){ans_nom[i] = fm[i].qur();ans[i] = mrg(pr[dfn[i] - 1], bh[dfn[i] + sz[i]]).qur();}int q;scanf_s("%d", &q);for (int i = 0; i < q; i++){int r, v;scanf_s("%d%d", &r, &v);if (r == 3 && v == 1){int u = 1;}int a=solve(r, v);printf("%d\n", a);}}
}