优化改进YOLOv5算法之改进用于微小目标检测的Normalized Gaussian Wasserstein Distance模块(超详细)
目录
1 Normalized Gaussian Wasserstein Distance
1.1 Motivation
1.2 方法
1.2.1 边界框的高斯分布建模
1.2.2 归一化的高斯Wasserstein距离
1.2.3 基于NWD的检测器
2 YOLOv5中添加NWD函数
参考文章
1 Normalized Gaussian Wasserstein Distance
论文链接:A Normalized Gaussian Wasserstein Distance for Tiny Object Detection
提出一个新的metric来测量边界框之间的相似性,用Wasserstein距离来代替标准的IoU。首先将边界框建模为二维高斯分布,然后用归一化的Wasserstein距离(NWD)来衡量高斯分布的相似性。Wasserstein距离最大的优点是即使两个边界框无重叠或相互包含,也可以测量分布的相似性。另外,NWD对不同尺度的目标不敏感,因此更适合测量极小目标间的相似性。
所提出的NWD可以同时用到单阶段和多阶段的检测器中。另外,NWD不仅可以代替标签分配中的IoU,而且也可以替代NMS和损失函数中的IoU。
1.1 Motivation
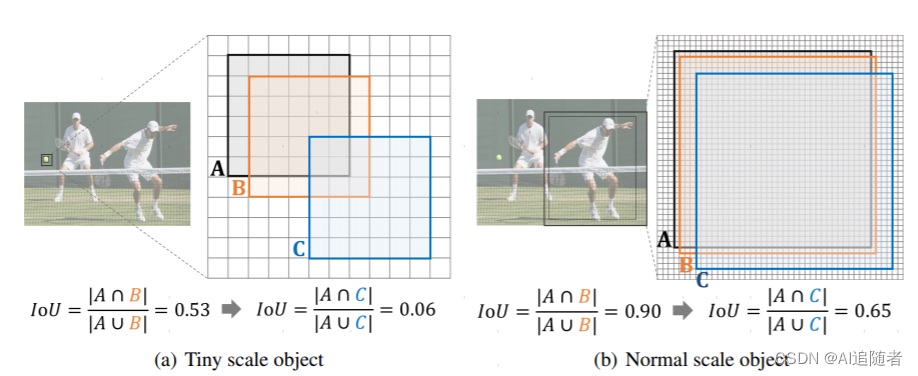
上图为极小目标和正常尺寸目标的IoU敏感性分析。注意每个格子代表一个像素,A表示一个GT边界框,B和C分别表示沿对角线偏移一个像素和四个像素的预测边界框。可以看到,对于极小目标检测,轻微的位置偏移就会造成IoU的下降。即使在正常的目标检测中,虽然没那么明显,但也有一定的下降。因此,需要设计新的metric来代替IoU,来衡量不同分布间的相似性。
1.2 方法
IoU实际上是计算两个有限样本集相似度的Jaccard相似系数,受此启发,作者提出一种基于Wasserstein距离的极小目标检测,因为它能在即使没有重叠的两个分布都能反映他们之间的距离。因此,Wasserstein距离在测量极小目标检测中比IoU有更好的特性。具体的细节如下:
1.2.1 边界框的高斯分布建模
对于极小目标,边界框中通常包含一些背景像素,因为大部分的真实目标不是严格的矩形。在这些边界框中,前景像素和背景像素分别集中在边界框的中心和边界。为了更好的描述边界框中的不同像素的权重,边界框可以被建模为两个二维的高斯分布,其中中心像素有最高的权重,然后从中心到边界像素的重要性递减。具体地,对于水平的边界框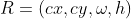 ,其中(cx,cy)、w、h分别表示边界框的中心点、宽和高。它的内切椭圆的公式为:
,其中(cx,cy)、w、h分别表示边界框的中心点、宽和高。它的内切椭圆的公式为:
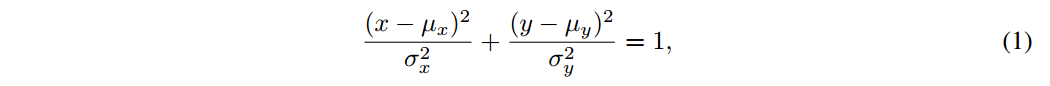
其中,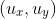 表示椭圆的中心坐标,
表示椭圆的中心坐标,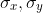 表示沿x轴和y半轴的长度。
表示沿x轴和y半轴的长度。
一个二维高斯分布的概率密度函数可以表示为:
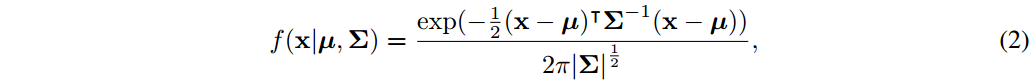
其中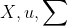 分别表示中心点(x,y),高斯分布的均值和协方差。
分别表示中心点(x,y),高斯分布的均值和协方差。
当
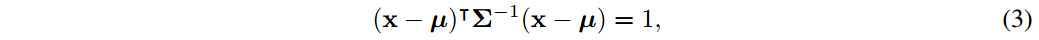
公式(1)中的椭圆则是二维高斯分布的密度轮廓。因此,水平边界框可以表示为一个二维高斯分布 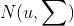 ,服从
,服从
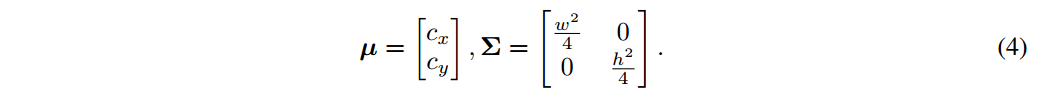
从而,两个边界框的相似度转化为两个高斯分布的距离分布。
1.2.2 归一化的高斯Wasserstein距离
Wasserstein距离来源于最佳传输理论,用来计算两个分布间的距离。对于两个高斯分布 和
和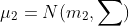 ,
,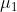 和
和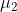 间的二阶Wasserstein距离可以定义为:
间的二阶Wasserstein距离可以定义为:
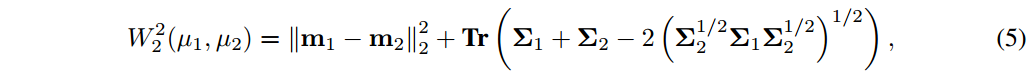
它可以简化为:
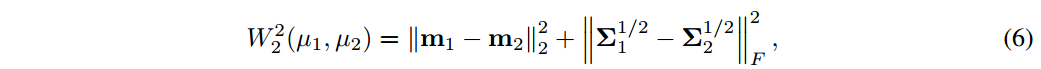
其中 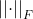 表示Frobenius范数
表示Frobenius范数
此外,公式(6)可以被更进一步简化为:
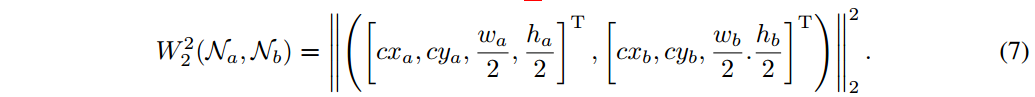
然而,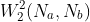 是一个距离度量,并不能直接用做相似性度量(也就是像IoU中是0-1间的数)。因此,作者采用指数的归一化形式,获得一个新的归一化Wasserstein距离(NWD):
是一个距离度量,并不能直接用做相似性度量(也就是像IoU中是0-1间的数)。因此,作者采用指数的归一化形式,获得一个新的归一化Wasserstein距离(NWD):
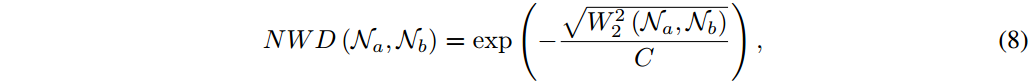
其中C是一个与数据集密切相关的常数。在实验中发现,设定C为AI-TOD中平均绝对尺寸能达到最好的检测性能。此外,可以发现C在一个特定的范围内是鲁棒的。
与IoU相比,NWD对于极小目标检测有以下优势:(1)尺度不变性;(2)对位置偏移的平滑性;(3)测量两个互不相交或相互包含的边界框的相似度。如图2所示,不是一般性,作者讨论了度量值在以下两种情形下的变化。
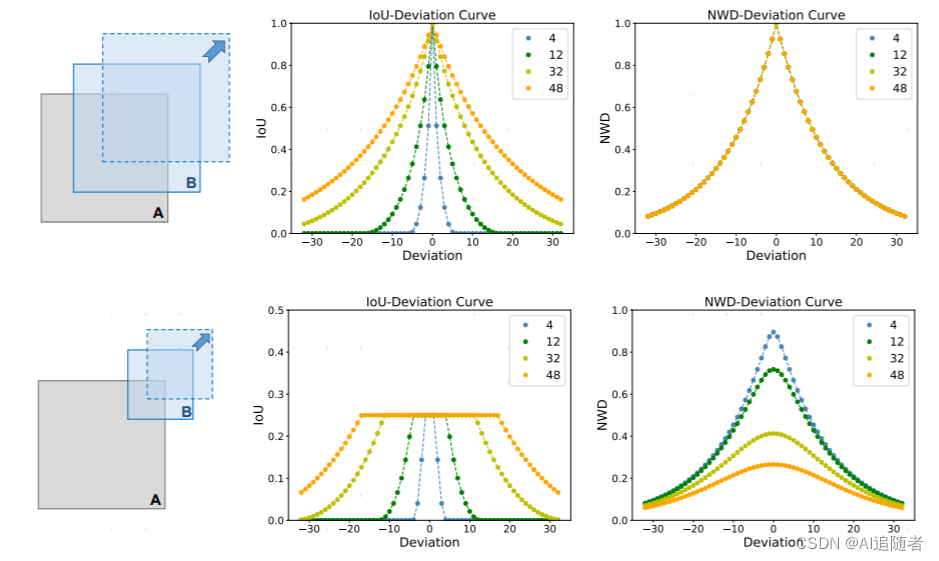
从图2的第一行中,保持边界框A和B尺度一样,将B沿着A的对角线移动。可以发现NWD的四个曲线是完全一致的,表明NWD对边界框的尺度变化是不敏感的。此外,发现IoU对于轻微的位置偏移很敏感,但由位置偏移导致的NWD变化更平滑。对位置偏移的平滑性表明,正负样本的区分比同样阈值的IoU要好。在图2的第二行,设B的边长是B边长的一半,沿着A的对角线移动B。相比IoU,NWD的曲线更平滑,它可以一致性的反映两个分布间的相似度,即使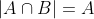 或
或 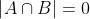 。
。
1.2.3 基于NWD的检测器
NWD可以很容易地代替IoU插入到任意anchor-based的检测器中。不失一般性,采用anchor-based Faster R-CNN来证明NWD的有效性。具体地,所有的修改都是在原来使用IoU的三个部分进行的。具体如下:
基于NWD的标签分配:Faster RCNN包含两个网络:RPN产生区域候选框,R-CNN在这些候选框基础上检测目标。RPN和R-CNN都包括标签分配过程。对于RPN,首先生成不同尺度和宽高比的anchors,然后将这些anchors分配二值标签用于训练后续的分类和回归。对于R-CNN,标签匹配过程与PRN类似,区别在于R-CNN的输入是RPN的输出。为了克服前边提到的IoU在极小目标检测中的缺点,作者设置了基于NWD的标签分配策略,利用NWD来分配标签。具体地,为了训练RPN,正标签将会被分配到两种anchors中:(1) 用GT框时,anchor具有最高的NWD值,这个值大于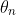 ;(2)任意GT框的anchor具有的NWD值都比正阈值
;(2)任意GT框的anchor具有的NWD值都比正阈值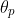 要高。相应地,如果NWD值小于负阈值
要高。相应地,如果NWD值小于负阈值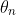 ,则被分为负样本。此外,既没有分配到正样本又没有分配到负样本的anchors将不会参与训练。注意,为了能够直接把NWD应用到anchor-based的检测器中,采用与原始检测器中同样的
,则被分为负样本。此外,既没有分配到正样本又没有分配到负样本的anchors将不会参与训练。注意,为了能够直接把NWD应用到anchor-based的检测器中,采用与原始检测器中同样的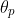 和
和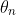 。
。
基于NWD的NMS:NMS是目标检测中不可分割的一部分,用来压缩冗余的预测框,其中用到了IoU。首先,根据他们的值将预测框进行排序。选择值最高的预测框M,将与之重叠度高的预测框删除(用预设的阈值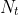 )。这个过程重复应用到余下的预测框中。然而,对极小目标的IoU的敏感性使得大量预测框的IoU的值低于
)。这个过程重复应用到余下的预测框中。然而,对极小目标的IoU的敏感性使得大量预测框的IoU的值低于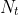 ,导致会产生很多假阳性预测。为了解决这个问题,作者在NMS中采用NWD,因为NWD克服了尺度敏感性问题。此外,基于NWD的NMS很灵活,可以应用到任意的极小目标检测中,只需要几行代码。
,导致会产生很多假阳性预测。为了解决这个问题,作者在NMS中采用NWD,因为NWD克服了尺度敏感性问题。此外,基于NWD的NMS很灵活,可以应用到任意的极小目标检测中,只需要几行代码。
基于NWD的损失函数:IoU-Loss被用来消除训练和测试间的性能差距。然而,IoU-Loss在以下两种情形中不能提供优化网络的梯度:(1) 预测框和GT框之间没有重叠(即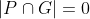 )或者二者相互包含(即
)或者二者相互包含(即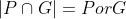 )。另外,这两种情况在极小目标中很常见。具体地,一方面,P中几个像素的偏离会引起P和G没有重叠。另一方面,极小目标很容易被误判,导致
)。另外,这两种情况在极小目标中很常见。具体地,一方面,P中几个像素的偏离会引起P和G没有重叠。另一方面,极小目标很容易被误判,导致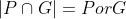 。因此,IoU-Loss并不适合极小目标的检测器。尽管CIoU 和DIoU能够解决以上两个问题,但依然对位置偏移敏感,因为他们都是基于IoU的。为了解决这些问题,作者设计了NWD损失:
。因此,IoU-Loss并不适合极小目标的检测器。尽管CIoU 和DIoU能够解决以上两个问题,但依然对位置偏移敏感,因为他们都是基于IoU的。为了解决这些问题,作者设计了NWD损失:
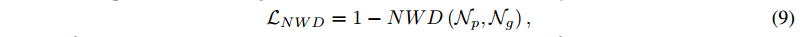
其中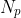 是预测框P的高斯分布模型,
是预测框P的高斯分布模型,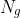 是GT框G的高斯分布模型。
是GT框G的高斯分布模型。
2 YOLOv5中添加NWD函数
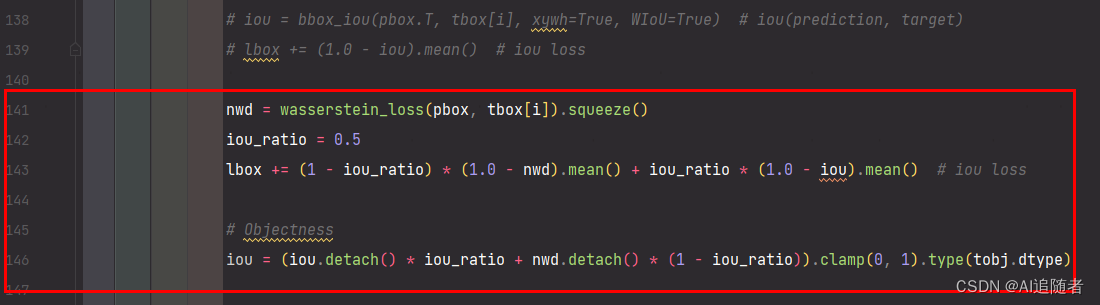
yolov5-6.1版本中的iou损失函数是在utils/metrics.py文件定义的,在该文件添加以下关于wasserstein_loss函数的代码,如下所示
def wasserstein_loss(pred, target, eps=1e-7, constant=12.8):r"""`Implementation of paper `Enhancing Geometric Factors intoModel Learning and Inference for Object Detection and InstanceSegmentation `_.Code is modified from https://github.com/Zzh-tju/CIoU.Args:pred (Tensor): Predicted bboxes of format (x1, y1, x2, y2),shape (n, 4).target (Tensor): Corresponding gt bboxes, shape (n, 4).eps (float): Eps to avoid log(0).Return:Tensor: Loss tensor."""center1 = pred[:, :2] + pred[:, 2:] / 2center2 = target[:, :2] + target[:, 2:] / 2whs = center1[:, :2] - center2[:, :2]center_distance = whs[:, 0] * whs[:, 0] + whs[:, 1] * whs[:, 1] + eps #w1 = pred[:, 2] + epsh1 = pred[:, 3] + epsw2 = target[:, 2] + epsh2 = target[:, 3] + epswh_distance = ((w1 - w2) ** 2 + (h1 - h2) ** 2) / 4wasserstein_2 = center_distance + wh_distancereturn torch.exp(-torch.sqrt(wasserstein_2) / constant) 然后在utils/loss.py文件中调用wasserstein_loss函数。
参考文章
航空遥感目标检测专题(10) - 知乎
提升小目标检测的一种新的包围框相似度度量:Normalized Gaussian Wasserstein Distance-技术圈
