文章目录

• • • Abstractions抽象
    • 半导体与集成电路
    • • Semiconductor Technology
    • 集成电路发明
    • • Intel Core i7 Wafer
      • Integrated Circuit Cost
      • Defining Performance
      • Response Time and Throughput
      • Relative Performance
      • Measuring Execution Time
      • CPU Clocking
      • CPU Time
      • • CPU Time Example
      • Instruction Count and CPI
      • CPI Example
      • CPI in More Detail
      • • CPI Example
      • Performance Summary
      • Power Trends
      • • Reducing Power
        • Multiprocessors（多核）
      • SPEC CPU Benchmark
      • SPEC Power Benchmark
      • Pitfall(陷阱): Amdahl’s Law
      • Fallacy谬误: Low Power at Idle
      • Pitfall: MIPS as a Performance Metric
      • Concluding Remarks

冯·诺依曼计算机

冯·诺依曼计算机由存储器、运算器、输入设备、输出设备和控制器五部分组成。

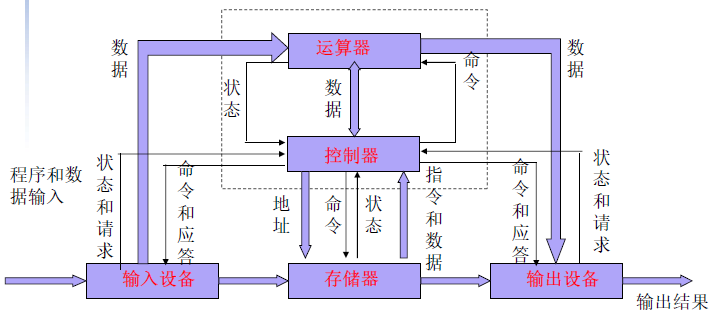
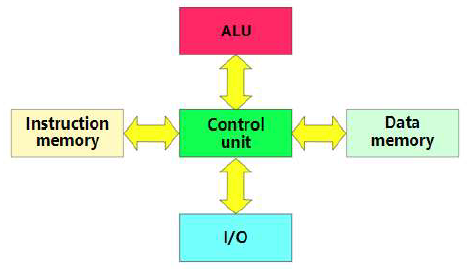
哈佛结构

哈佛结构是一种将程序指令存储和数据存储分开的存储器结构，它的主要特点是将程序和数据存储在不同的存储空间中，即程序存储器和数据存储器是两个独立的存储器，每个存储器独立编址、独立访问，目的是为了减轻程序运行时的访存瓶颈。哈佛架构的中央处理器典型代表ARM9/10及后续ARMv8的处理器，例如：华为鲲鹏920处理器。

组成计算机的基础硬件都需要与主板（Motherboard）连接

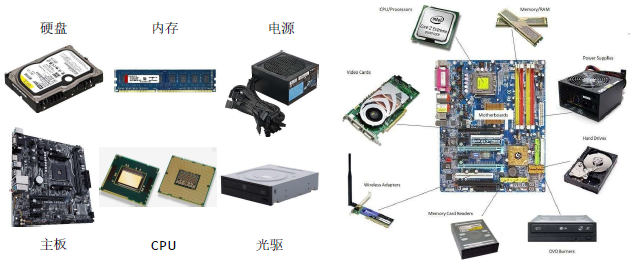
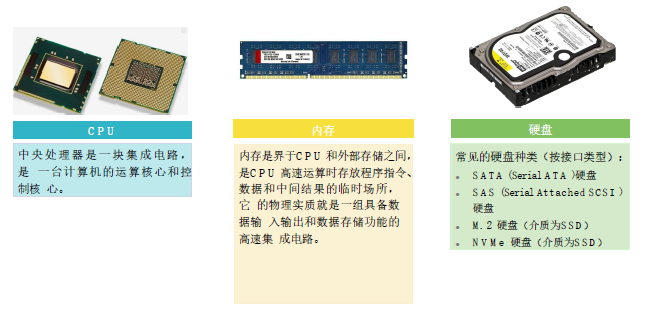
计算机基础硬件 (2)

Opening the Box（Apple IPad2）

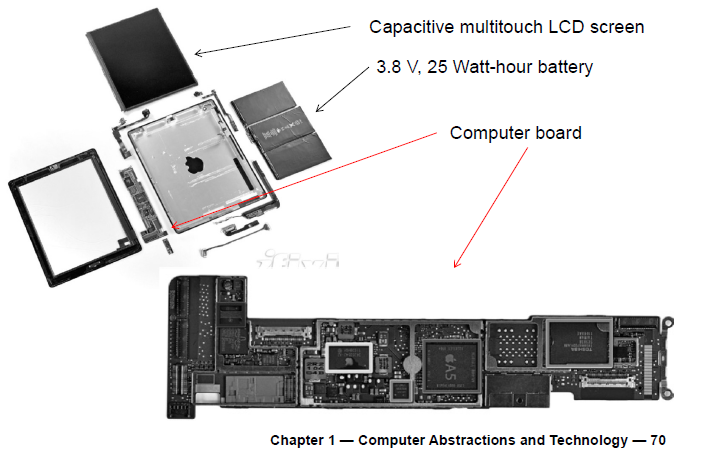
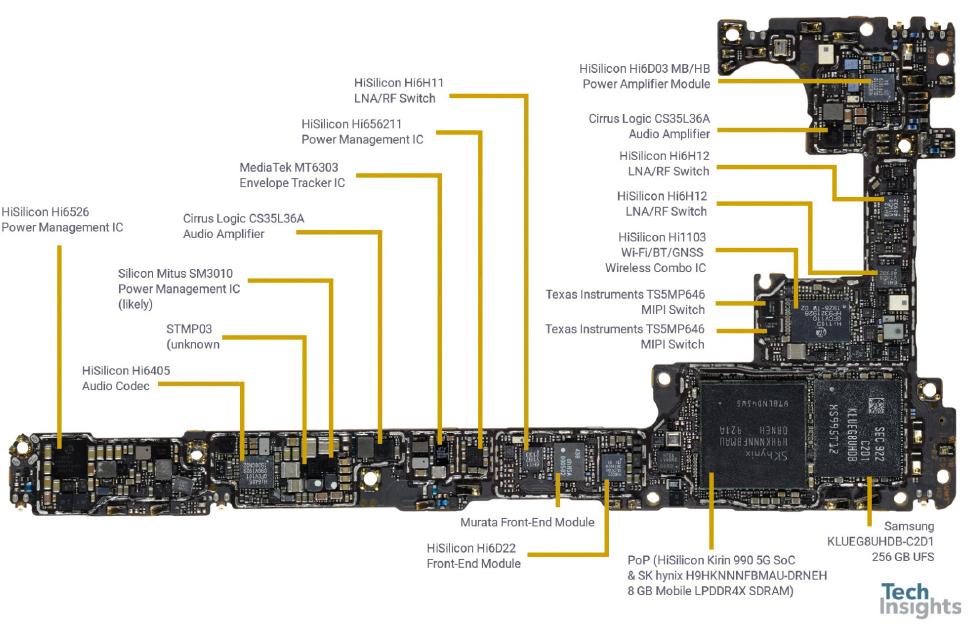
手机的内部结构 – 华为Mate30 Pro

主板(来自于 Tech Insights）

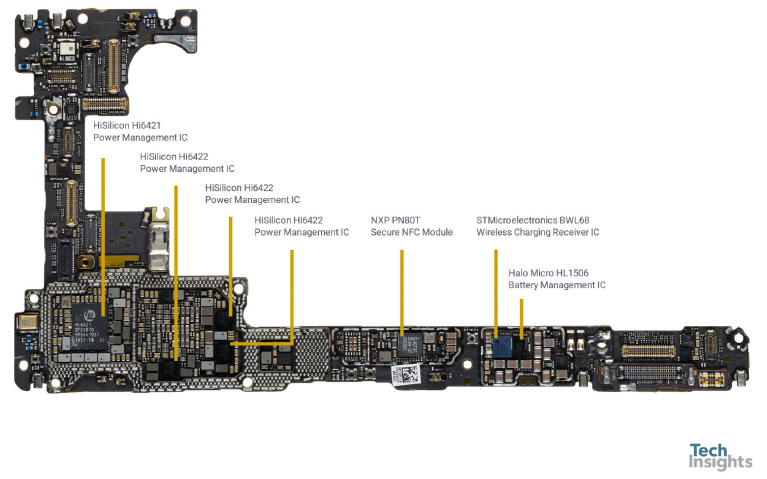
主板 背面

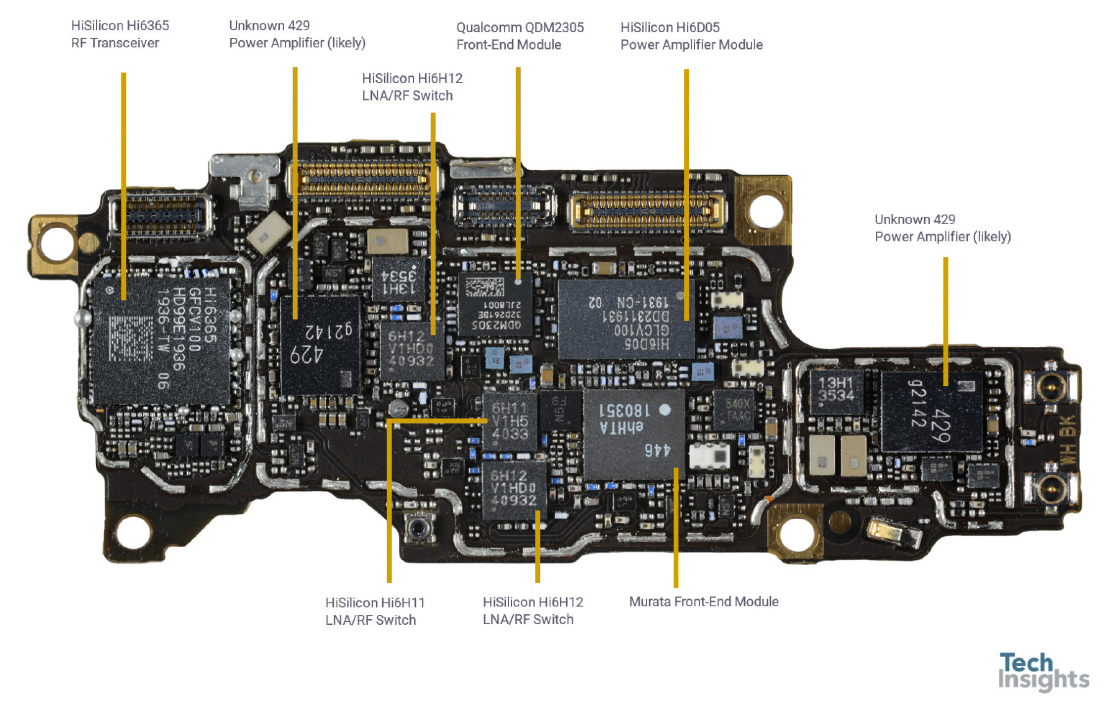
射频板

Inside the Processor (CPU)

• Datapath(数据通路): performs operationson data
• Control: sequences datapath, memory, …
• Register 寄存器
• Cache memory 缓存
  • Small， fast： SRAM(静态随机访问存储器)
    memory for immediate access to data

Intel Core i7-5960X

毅力号CPU曝光：250nm工艺、23年旧架构、主频仅233MHz

毅力号搭载的处理器是20多年前技术的产品。处理器型号为PowerPC 750处理器，与1998年苹果出品的iMac G3 电脑同款，PowerPC 750 处理器最高主频速度仅233MHz，且晶体管数量也只有600 万个，但单价仍高达20 万美元（约130万元）。抗辐射、耐寒冷-55~125℃

对比苹果最近推出的M1ARM 架构处理器拥有最高主频3.2GHz，晶体管数量达160 亿个。

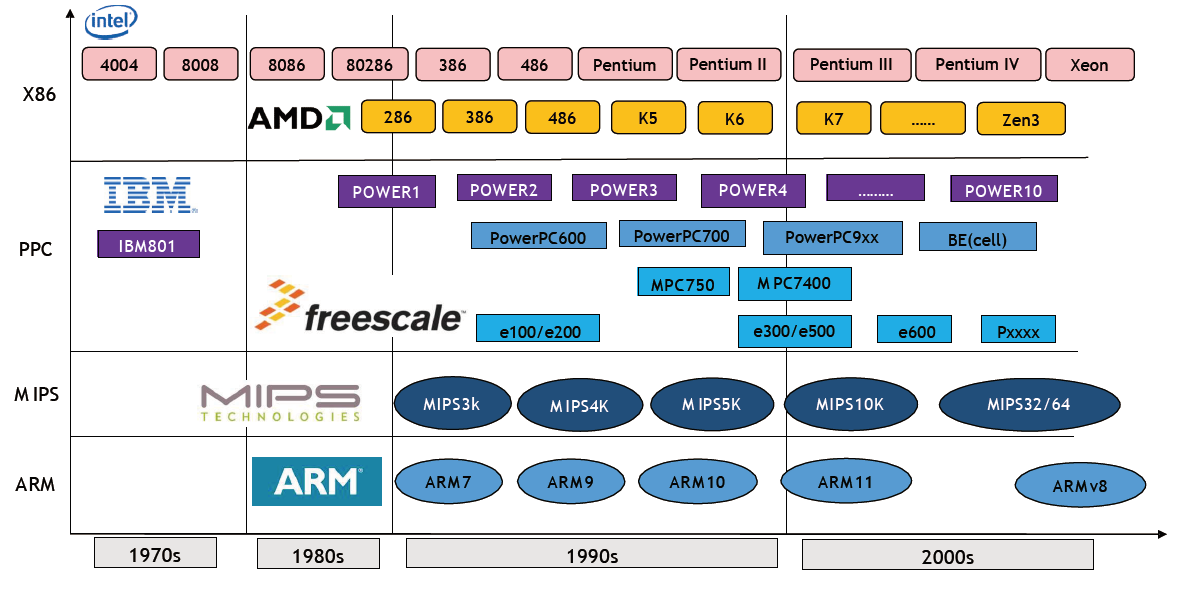
处理器发展趋势

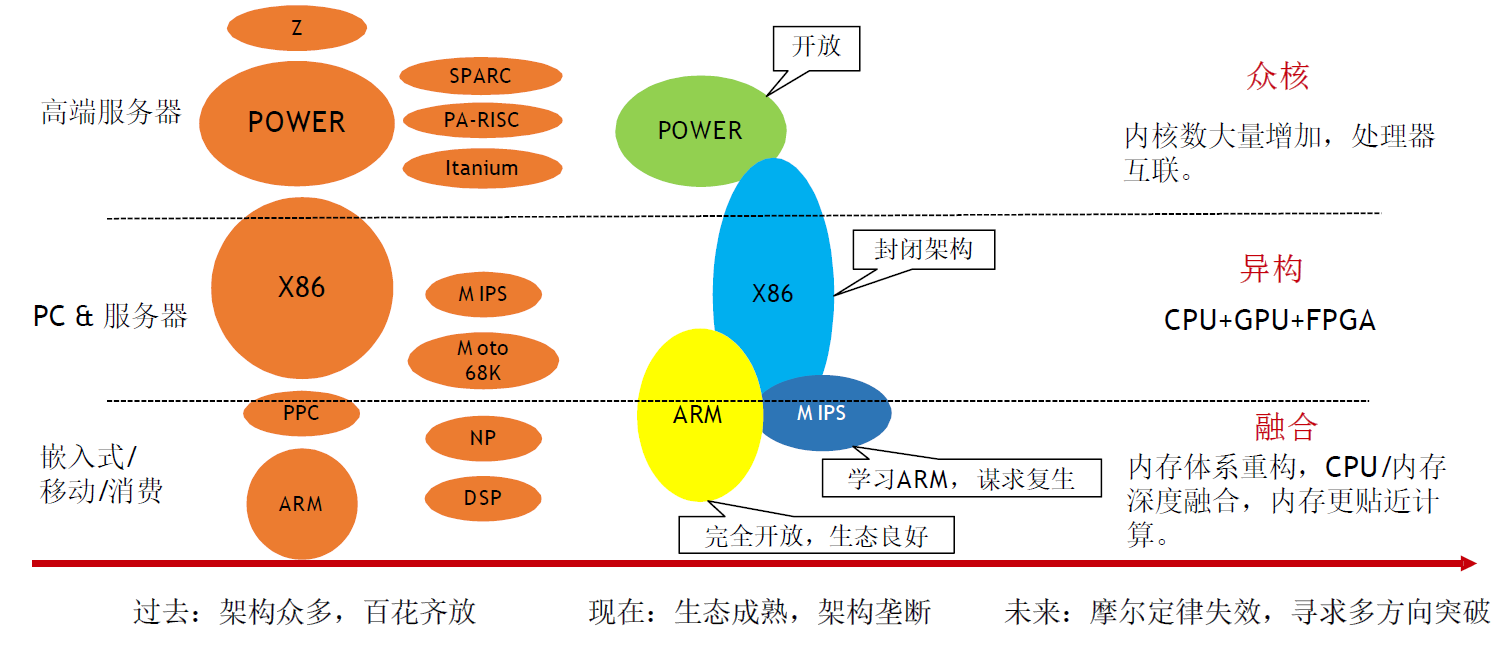
主流CPU发展路径

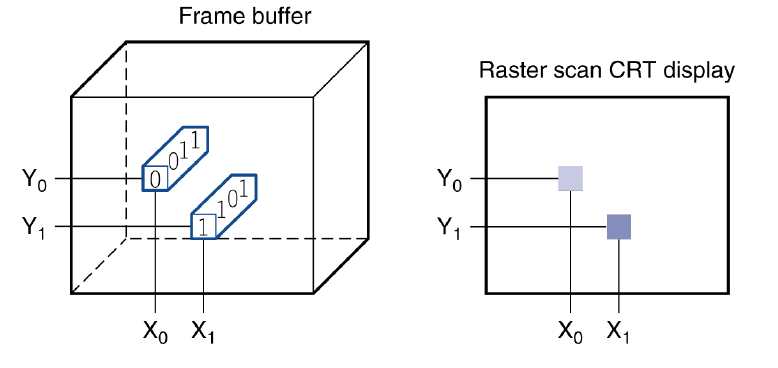
Through the Looking Glass

LCD screen: picture elements (pixels像素)

• Mirrors content of frame buffer memory帧缓冲存储器

Touchscreen(触摸屏)

PostPC device

• Supersedes(取代)keyboard and mouse
• Resistive阻性 and Capacitive容性types
  • Most tablets, smart phones use capacitive
  • Capacitive allows multiple touches simultaneously(多点同时触控)

A Safe Place for Data

Volatile main memory(易失性主存)

• Loses instructions and data when power off(断电)

Non-volatile secondary memory

• Magnetic disk(磁盘)
• Flash memory(闪存)
• Optical disk (CDROM, DVD) 光盘

Networks 与其他计算机通信

• Communication(通信), resource sharing(资源共享), nonlocal access(远程访问)

• Local area network (LAN): Ethernet,局域网/以太网

• Wide area network (WAN): the Internet，广域网/互联网

• Wireless network: WiFi, Bluetooth(蓝牙)

计算机基础硬件 (3)

Abstractions抽象

The BIG Picture

• Abstraction helps us deal with complexity
  • Hide lower-level detail
• Instruction set architecture (ISA)指令集体系结构
  • The hardware/software (abstraction) interface
• Application< ---- > binary interface应用二进制接口
  • The ISA plus system software interface
• Implementation(区别于Architecture)
  • The details underlying the interface

半导体与集成电路

Technology Trends 处理器和存储器制造技术–趋势

Electronics technology continues to evolve

• Increased capacity and performance
• Reduced cost

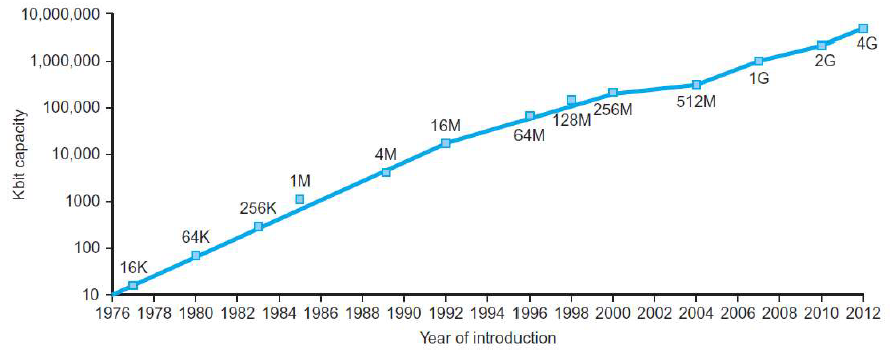
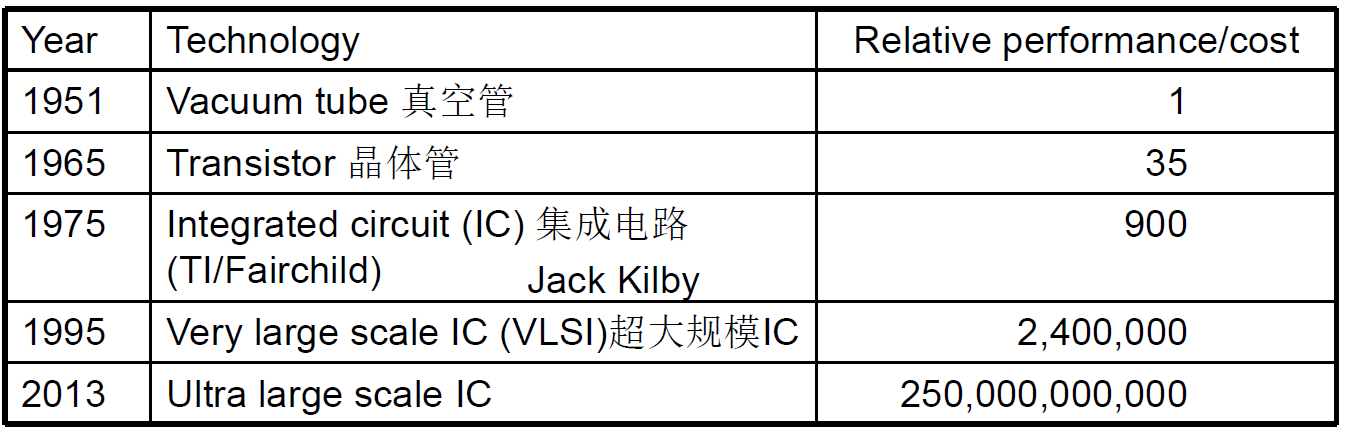
Semiconductor Technology

• Silicon硅: semiconductor 半导体
• Add materials to transform properties属性:
  • Conductors
  • Insulators
  • Switch

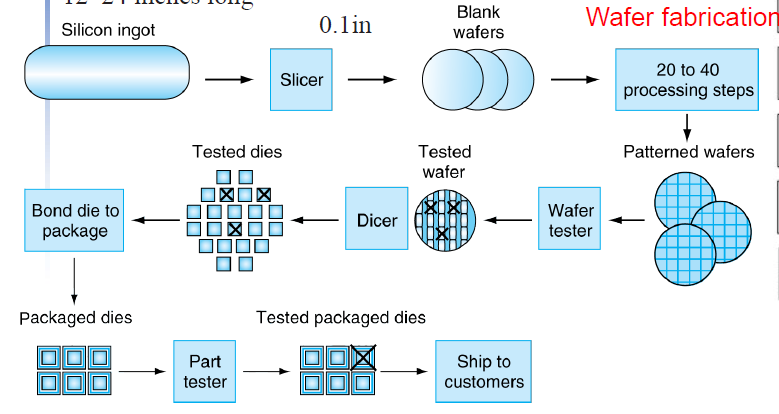
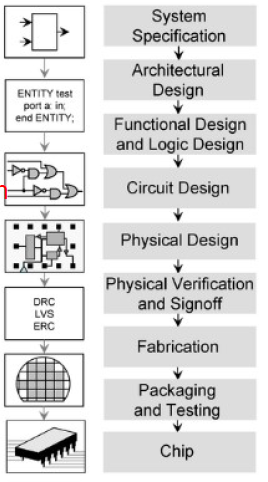
设备列表

厂商在制造芯片的过程中，从前端工序、到晶圆制造工序，之后再到封装和测试工序，主要用到的设备依次包括，单晶炉、气相外延炉、氧化炉、低压化学气相沉积系统、磁控溅射台、光刻机、刻蚀机、离子注入机、晶片减薄机、晶圆划片机、键合封装设备、测试机、分选机和探针台等

集成电路发明

• 1952年，英国雷达研究所的科学家达默在一次会议上提出：可以把电子线路中的分立元器件，集中制作在一块半导体晶片上，一小块晶片就是一个完整电路，这样一来，电子线路的体积就可大大缩小，可靠性大幅提高。这就是初期集成电路的构想。

• 1956年，美国材料科学专家富勒和赖斯发明了半导体生产的扩散工艺，这样就为发明集成电路提供了工艺技术基础。

• 1958年9月，美国德州仪器公司的青年工程师杰克·基尔比（Jack Kilby），成功地将包括锗晶体管在内的五个元器件集成在一起，基于锗材料制作了一个叫做相移振荡器的简易集成电路，并于1959年2月申请了小型化的电子电路（Miniaturized Electronic Circuit）专利（专利号为No.31838743，批准时间为1964年6月26日），这就是世界上第一块锗集成电路。

• 2000年，集成电路问世42年以后，人们终于了解到他和他的发明的价值，他被授予了诺贝尔物理学奖。诺贝尔奖评审委员会曾经这样评价基尔比：“为现代信息技术奠定了基础”。

• 1959年7月，美国仙童半导体公司的诺伊斯，研究出一种利用二氧化硅屏蔽的扩散技术和PN结隔离技术，基于硅平面工艺发明了世界上第一块硅集成电路，并申请了基于硅平面工艺的集成电路发明专利（专利号为No.2981877，批准时间为1961年4月26日。虽然诺伊斯申请专利在基尔比之后，但批准在前）。

• 基尔比和诺伊斯几乎在同一时间分别发明了集成电路，两人均被认为是集成电路的发明者，而诺伊斯发明的硅集成电路更适于商业化生产，使集成电路从此进入商业规模化生产阶段。

Intel Core i7 Wafer

• 300mm wafer, 280 chips, 32nm technology
• Each chip is 20.7 x 10.5 mm

Integrated Circuit Cost

Costperdie=Cost per wafer Dies per wafer ×Yield Cost per die =\frac{\text { Cost per wafer }}{\text { Dies per wafer } \times \text { Yield }}Costperdie= Dies per wafer × Yield  Cost per wafer ​

Diesperwafer≈Waferarea/DieareaDies per wafer \approx Wafer area/Die areaDiesperwafer≈Waferarea/Diearea

Yield=1(1+(Defects per area ×Die area /2))2Yield =\frac{1}{(1+(\text { Defects per area } \times \text { Die area } / 2))^{2}}Yield=(1+( Defects per area × Die area /2))21​

成品率

Defects per area：单位面积缺陷

Die area：模具面积

Defining Performance

• Which airplane has the best performance? 从不同的方面进行考察。

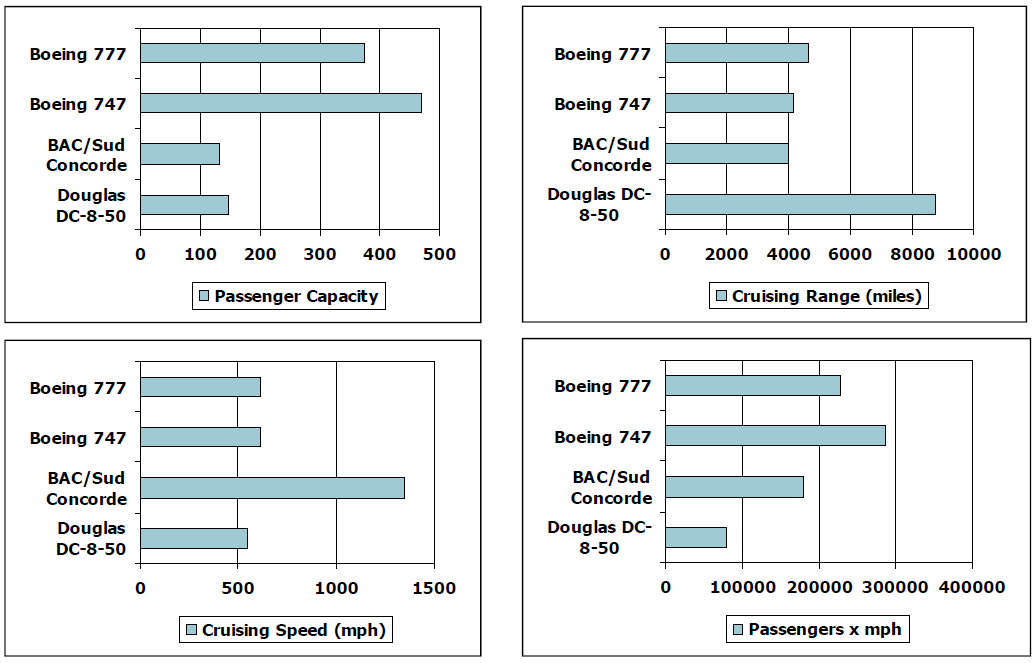
Response Time and Throughput

• Response time响应时间
  • How long it takes to do a task(the time between the start and completion of a task)
• Throughput吞吐量
  • Total work done per unit time
  • e.g., tasks/transactions/… per hour
• How are response time and throughput affected by
  • Replacing the processor with a faster version? 改善处理器
  • Adding more processors to do separate tasks? 添加更多的处理器
  • Queue ？采用排队机制，改善吞吐量
• We’ll focus on response time for now…

Relative Performance

Define Performance = 1/Execution Time

• “X is n time faster than Y”
• $Performance _{X} / Performance _{Y}
  = Execution time _{Y} / Execution time _{X}=n $

Example: time taken to run a program

• 10s on A, 15s on B
• Execution TimeB / Execution TimeA = 15s / 10s = 1.5
• So A is 1.5 times faster than B

Measuring Execution Time

• Elapsed time 消逝时间
  • Total response time, including all aspects
    • Processing, I/O, OS overhead, idle time
  • Determines system performance
• CPU time（共享时,独自占用CPU时间）
  • Time spent processing a given job
    • Discounts I/O time, other jobs’ shares
  • Comprises user CPU time and system CPU
    time
  • Different programs are affected differently by
    CPU and system performance

CPU Clocking

Operation of digital hardware governed(掌控) by a constant-rate clock （数字同步电路）

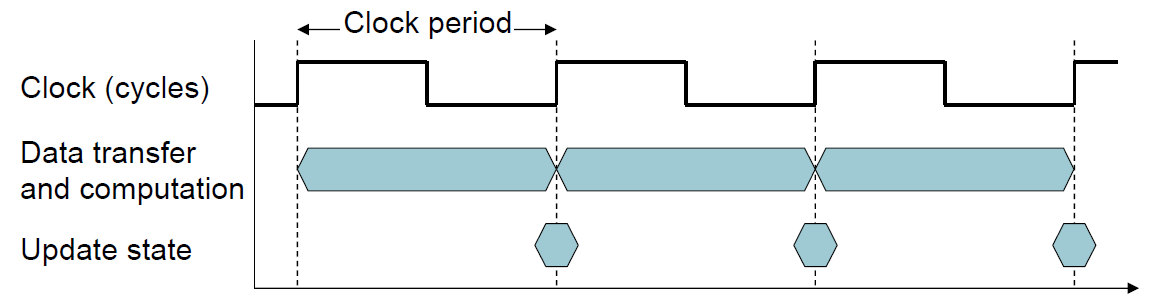
• Clock period: duration of a clock cycle
  • e.g., 250ps = 0.25ns = 250×10^–12s
• Clock frequency (rate): cycles per second
  • e.g., 4.0GHz = 4000MHz = 4.0×10^9Hz

CPU Time

CPU Time = CPU Clock Cycles x Clock Cycle Time =CPU Clock Cycles Clock Rate \frac{\text { CPU Clock Cycles }}{\text { Clock Rate }} Clock Rate  CPU Clock Cycles ​

Performance improved by

• Reducing number of clock cycles
• Increasing clock rate
• Hardware designer must often trade off(折中)clock rate against cycle count

CPU Time Example

• Computer A: 2GHz clock, 10s CPU time
• Designing Computer B
  • Aim for 6s CPU time
  • Can do faster clock, but causes 1.2 × clock cycles
• How fast must Computer B clock be?

ClockCyclesA=CPUTimeA×ClockRateAClock Cycles _{A}= CPU Time _{A} \times Clock Rate _{A}ClockCyclesA​=CPUTimeA​×ClockRateA​

=10s×2GHz=20×10910 \mathrm{~s} \times 2 \mathrm{GHz}=20 \times 10^{9}10 s×2GHz=20×109

=1.2×20×1096s=24×1096s=4GHz\frac{1.2 \times 20 \times 10^{9}}{6 \mathrm{~s}}=\frac{24 \times 10^{9}}{6 \mathrm{~s}}=4 \mathrm{GHz}6 s1.2×20×109​=6 s24×109​=4GHz

Instruction Count and CPI

ClockCycles=InstructionCount×CyclesperInstructionClock Cycles = Instruction Count \times Cycles per InstructionClockCycles=InstructionCount×CyclesperInstruction

CPUTime=InstructionCount×CPI×ClockCycleTimeCPUTime = Instruction Count \times CPI \times Clock Cycle TimeCPUTime=InstructionCount×CPI×ClockCycleTime

=Instruction Count ×CPIClock Rate =\frac{\text { Instruction Count } \times \mathrm{CPI}}{\text { Clock Rate }}= Clock Rate  Instruction Count ×CPI​

• Instruction Count for a program
  • Determined by program, ISA and compiler
• Average cycles per instruction
  • Determined by CPU hardware
  • If different instructions have different CPI 指令具有不同CPI
    • Average CPI affected by instruction mix

CPI Example

• Computer A: Cycle Time = 250ps, CPI = 2.0
• Computer B: Cycle Time = 500ps, CPI = 1.2
• Same ISA
• Which is faster, and by how much?

CPI in More Detail

If different instruction classes take different numbers 每指令类CPI不同，且指令出现频率不同

Clock Cycles =∑i=1n(CPIi×Instruction Count ⁡i)\text { Clock Cycles }=\sum_{\mathrm{i}=1}^{n}\left(\mathrm{CPI}_{\mathrm{i}} \times \operatorname{Instruction~Count~}_{\mathrm{i}}\right) Clock Cycles =∑i=1n​(CPIi​×Instruction Count i​)

Weighted average CPI(平均CPI)

CPI=Clock Cycles Instruction Count =∑i=1n(CPIi×Instruction Count iInstruction Count )\mathrm{CPI}=\frac{\text { Clock Cycles }}{\text { Instruction Count }}=\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{CPI}_{\mathrm{i}} \times \frac{\text { Instruction Count }_{\mathrm{i}}}{\text { Instruction Count }}\right)CPI= Instruction Count  Clock Cycles ​=∑i=1n​(CPIi​× Instruction Count  Instruction Count i​​)

CPI Example

Alternative compiled code sequences using instructions in classes A, B, C (三类指令)

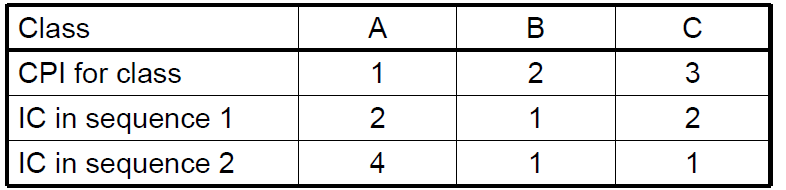
Which code sequence executes the most instructions? sequence2

Which will be faster?

What is the CPI for each sequence?

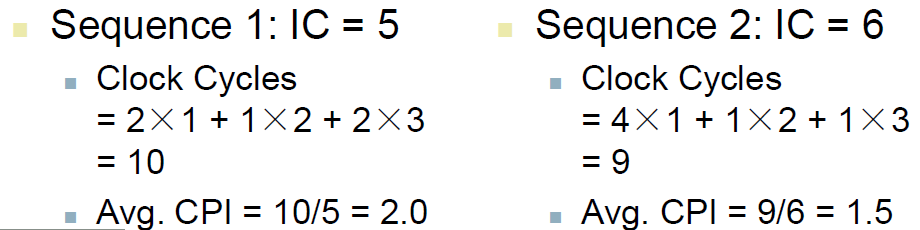
Performance Summary

CPU Time =Instructions Program ×Clock cycles Instruction ×Seconds Clock cycle \text { CPU Time }=\frac{\text { Instructions }}{\text { Program }} \times \frac{\text { Clock cycles }}{\text { Instruction }} \times \frac{\text { Seconds }}{\text { Clock cycle }} CPU Time = Program  Instructions ​× Instruction  Clock cycles ​× Clock cycle  Seconds ​

Performance depends on

• Algorithm: affects IC(指令数), possibly CPI
• Programming language: affects IC, CPI
• Compiler: affects IC, CPI
• Instruction set architecture: affects IC, CPI, Tc

Power Trends

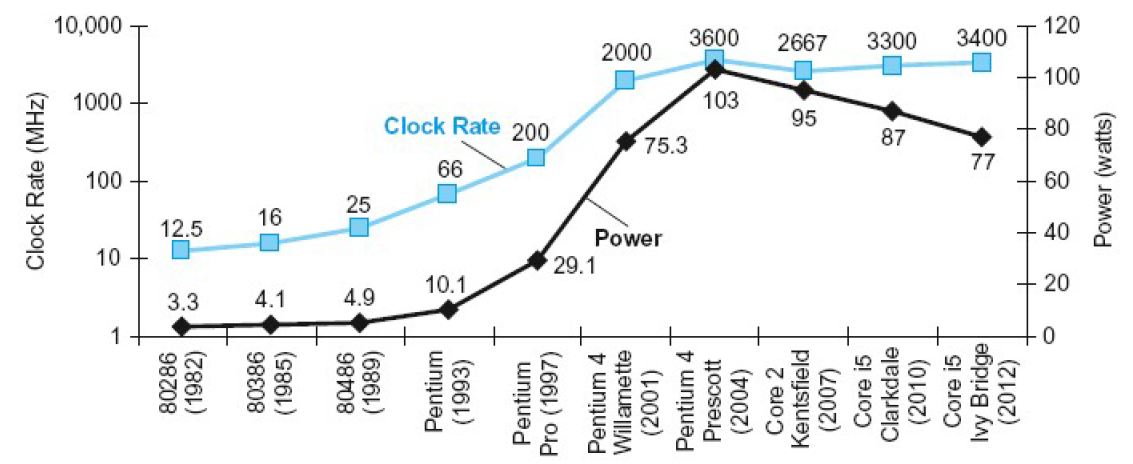
In CMOS IC technology

Power =12Capacitive load ×Voltage 2×Frequency \text { Power }=\frac{1}{2} \text { Capacitive load } \times \text { Voltage }^{2} \times \text { Frequency } Power =21​ Capacitive load × Voltage 2× Frequency 

Capacitive load:负载电容。

Reducing Power

Suppose a new CPU has

• 85% of capacitive load of old CPU
• 15% voltage and 15% frequency reduction

Pnew Pold =Cold ×0.85×(Vold ×0.85)2×Fold ×0.85Cold ×Vold 2×Fold =0.854=0.52\frac{P_{\text {new }}}{P_{\text {old }}}=\frac{C_{\text {old }} \times 0.85 \times\left(V_{\text {old }} \times 0.85\right)^{2} \times F_{\text {old }} \times 0.85}{C_{\text {old }} \times V_{\text {old }}^{2} \times F_{\text {old }}}=0.85^{4}=0.52Pold ​Pnew ​​=Cold ​×Vold 2​×Fold ​Cold ​×0.85×(Vold ​×0.85)2×Fold ​×0.85​=0.854=0.52

• The power wall (功率墙)
  • We can’t reduce voltage further 可能低压泄露
  • We can’t remove more heat 可能sleep
• How else can we improve performance?

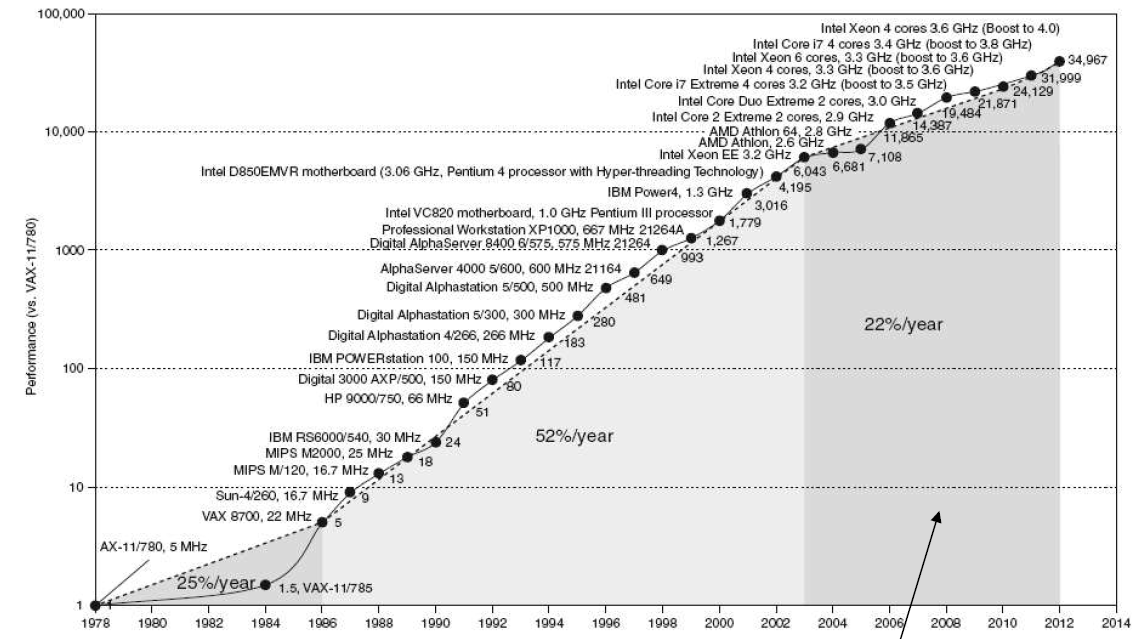
Constrained by power, instruction-level parallelism, memory latency（受到功率、指令级并行性、内存延迟的制约）

Multiprocessors（多核）

• Multicore microprocessors
  • More than one processor per chip
• Requires explicitly parallel programming
  • Compare with instruction level parallelism(e.g.流水线）
    • Hardware executes multiple instructions at once
    • Hidden from the programmer (程序员不可见)
• Hard to do
  • Programming for performance 编程难度增加
  • Load balancing 负载均衡
  • Optimizing communication and synchronization

A R M提供更多计算核心

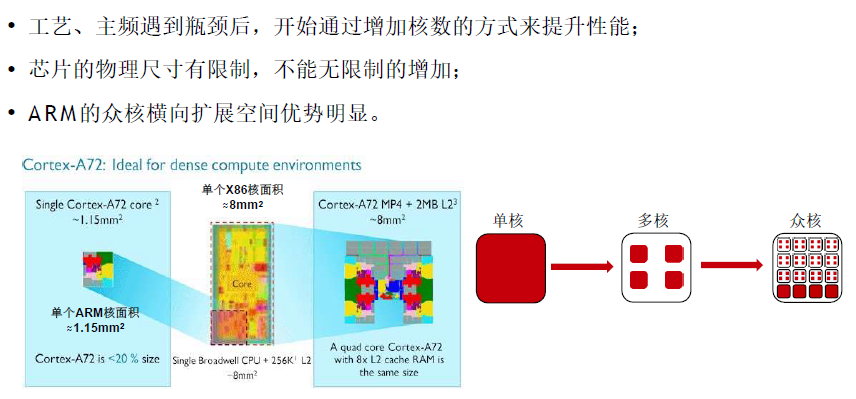
多核架构单位芯片面积提供更强算力，更符合分布式业务的需求

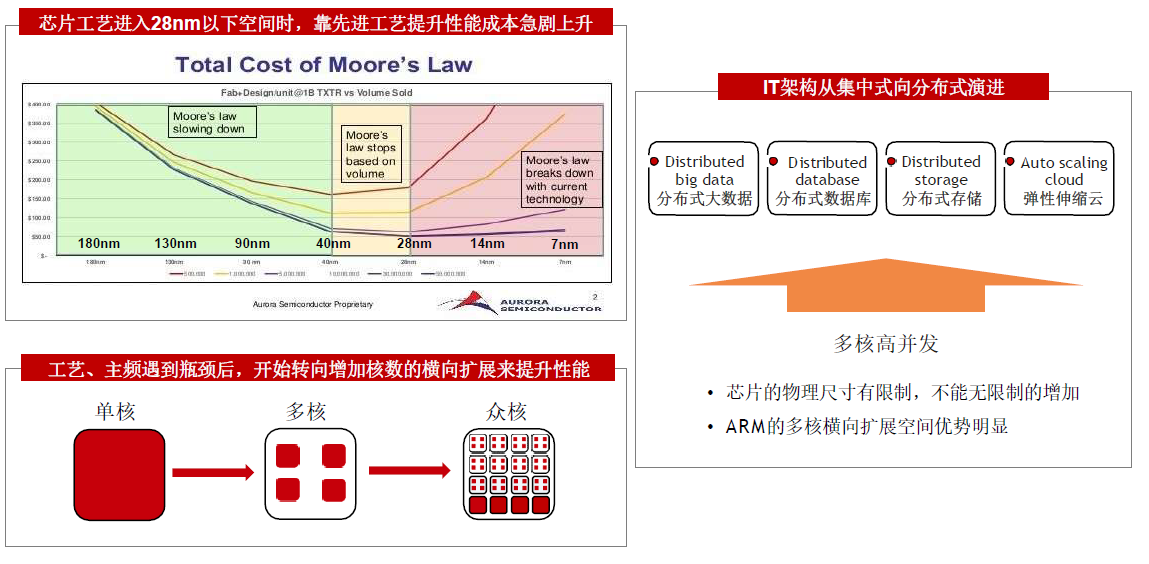
A R M多核高并发优势，匹配互联网分布式架构

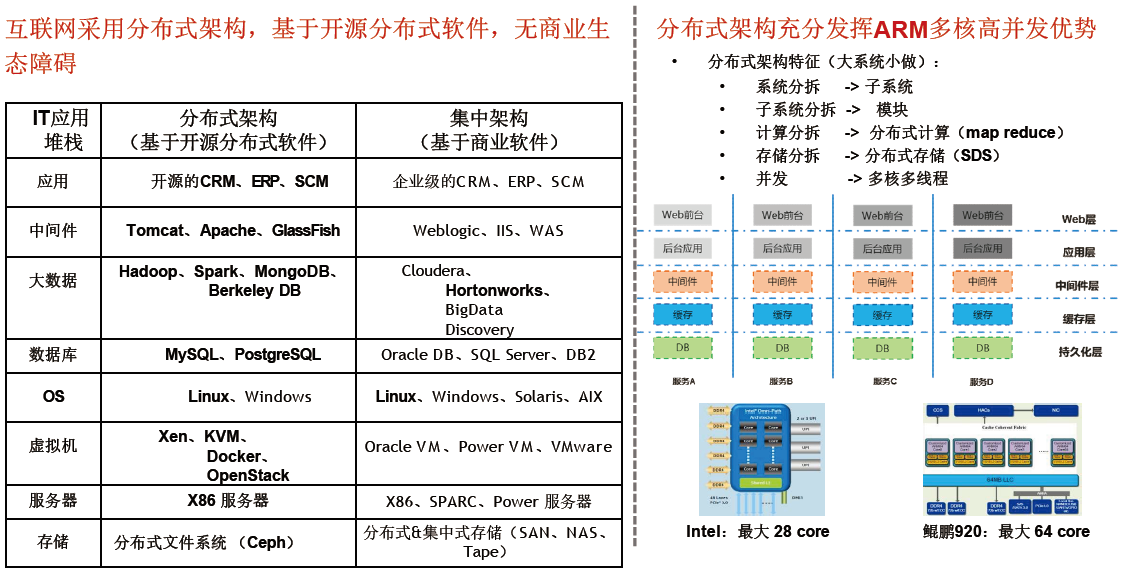
随着多核A R M CPU的性能不断增强，应用领域不断扩展

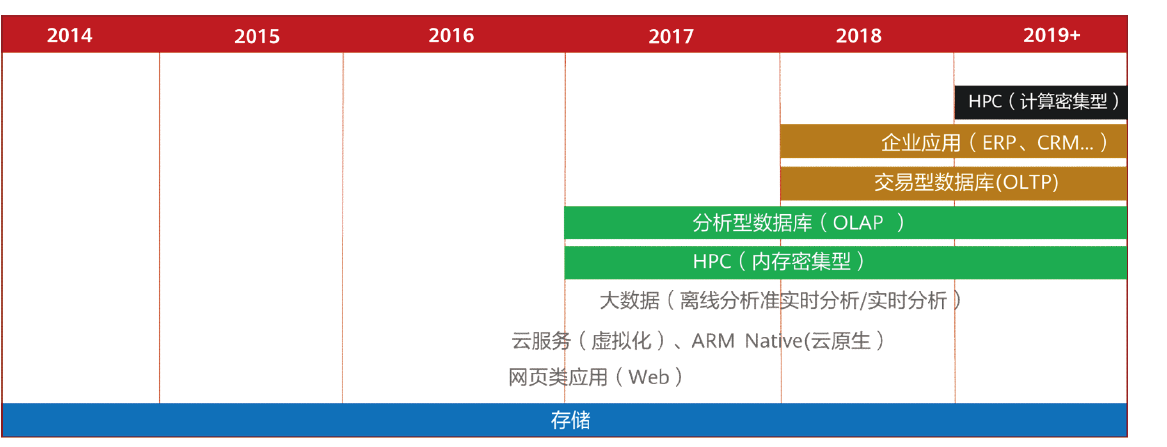
A R M服务器级别处理器一览

SPEC CPU Benchmark

• Programs used to measure performance
  • Supposedly typical of actual workload
• Standard Performance Evaluation Corp (SPEC)
  • Develops benchmarks for CPU, I/O, Web, …
• SPEC CPU2006
  • Elapsed time to execute a selection of programs
    • Negligible I/O, so focuses on CPU performance
  • Normalize relative to reference machine（参考机器）
  • Summarize as geometric mean of performance ratios
    • CINT2006 (integer) and CFP2006 (floating-point)

∏i=1nExecution time ratio in\sqrt[n]{\prod_{\mathrm{i}=1}^{n} \text { Execution time ratio }_{i}}n∏i=1n​ Execution time ratio i​​

CINT2006 for Intel Core i7 920

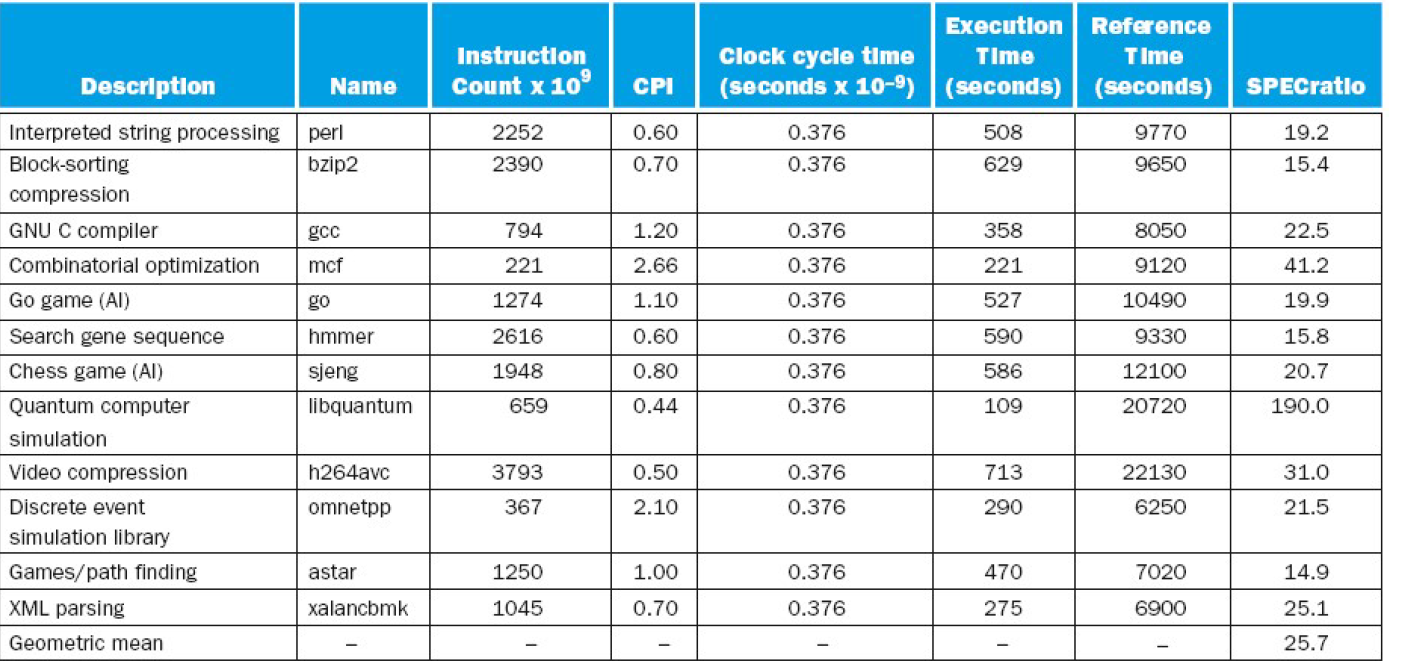
SPEC Power Benchmark

Power consumption of server at different workload levels

• Performance: ssj_ops/sec
• Power: Watts (Joules/sec)

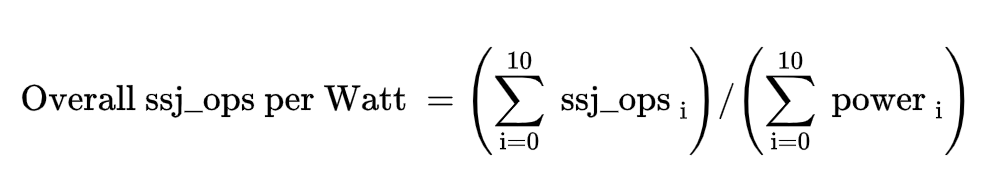
SPECpower_ssj2008 for Xeon X5650

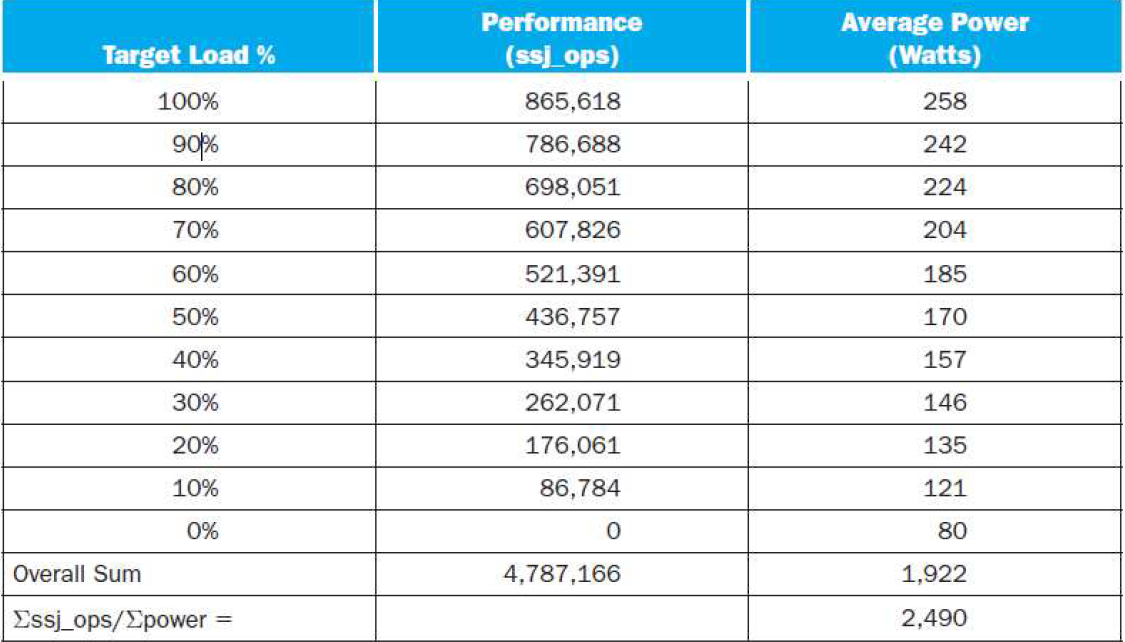
Pitfall(陷阱): Amdahl’s Law

Improving an aspect of a computer and expecting a proportional improvement in overall performance

Timproved =Taffected improvement factor +Tunaffected T_{\text {improved }}=\frac{T_{\text {affected }}}{\text { improvement factor }}+T_{\text {unaffected }}Timproved ​= improvement factor Taffected ​​+Tunaffected ​

Example: multiply accounts for 80s/100s

Speedup(E)=1/{(1-P)+P/S}

Amdahl’s law主要的用`途是指出了在计算机体系结构设计过程中，某个部件的优化对整个结构的优化帮助是有上限的，这个极限就是当S->时, speedup(E)= 1/(1-P);也从另外一个方面说明了在体系结构的优化设计过程中，应该挑选对整体有重大影响的部件来进行优化，以得到更好的结果。

Fallacy谬误: Low Power at Idle

Look back at i7 power benchmark

• At 100% load: 258W
• At 50% load: 170W (66%)
• At 10% load: 121W (47%)

Google data center

• Mostly operates at 10% – 50% load
• At 100% load less than 1% of the time

Consider designing processors to make power proportional to load

Pitfall: MIPS as a Performance Metric

MIPS: Millions of Instructions Per Second

• Doesn’t account for 考虑

  • Differences in ISAs between computers
  • Differences in complexity between instructions

• MIPS =Instruction count Execution time ×106=Instruction count Instruction count ×CPIClock rate ×106=Clock rate CPI×106\begin{aligned} \text { MIPS } &=\frac{\text { Instruction count }}{\text { Execution time } \times 10^{6}} \\ &=\frac{\text { Instruction count }}{\frac{\text { Instruction count } \times \mathrm{CPI}}{\text { Clock rate }} \times 10^{6}}=\frac{\text { Clock rate }}{\mathrm{CPI} \times 10^{6}} \end{aligned} MIPS ​= Execution time ×106 Instruction count ​= Clock rate  Instruction count ×CPI​×106 Instruction count ​=CPI×106 Clock rate ​​

• CPI varies between programs on a given CPU

Concluding Remarks

Cost/performance is improving

• Due to underlying technology development

Hierarchical layers of abstraction

• In both hardware and software

Instruction set architecture

• The hardware/software interface

Execution time: the best performance measure

Power is a limiting factor

• Use parallelism to improve performance