文章目录

• 随机过程 Poisson 过程
• • 基本概念
  • 与 Poisson 过程相联系的若干分布
  • • XnX_nXn​ 和 TnT_nTn​ 的分布
    • 事件发生各时刻的条件分布
  • Poisson 过程的推广
  • • 非齐次 Poisson 过程
    • 复合 Poisson 过程
    • 条件 Poisson 过程

随机过程 Poisson 过程

基本概念

（这里介绍了 Poisson 过程的两种定义方法）

计数过程：随机过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 称为计数过程，如果 N(t)N(t)N(t) 表示从 000 到 ttt 时刻某一特定时间 AAA 发生的次数，它具备以下两个特点：

• N(t)≥0N(t)\geq 0N(t)≥0 且取值为整数；
• 当 s

Poisson 过程：计数过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 被称为参数为 λ\lambdaλ（λ>0\lambda\gt 0λ>0）的 Poisson 过程，如果：

• N(0)=0N(0)=0N(0)=0 ；
• 过程有独立增量
• 在任一长度为 ttt 的时间区间中事件发生的次数服从均值为 λt\lambda tλt 的 Poisson 分布，即对一切 s≥0s\geq 0s≥0 ，t>0t \gt 0t>0 ，有

P(N(t+s)−N(s)=n)=e−λt(λt)nn!,n=0,1,2,⋯P(N(t+s)-N(s)=n)=e^{-\lambda t}\frac{(\lambda t)^n}{n!},\quad n=0,\,1,\,2,\,\cdots P(N(t+s)−N(s)=n)=e−λtn!(λt)n​,n=0,1,2,⋯

Poisson 过程的特点：

• 从第三点可以看出，任意 ttt 时间间隔内的分布与起始时间 sss 无关，因此 Poisson 过程具有平稳增量性；
• λ\lambdaλ 可以看作单位时间内事件发生的平均次数，一般被称为强度、速率或发生率

例：某火车站售票处早上 8：00 开始营业，乘客以 101010 人/小时的平均速率到达，则 9：10~10：00 这 1 个小时内最多有 5 名乘客来此购票的概率是多少？10：00~11:00 没有人来买票的概率是多少？

解：我们用一个泊松过程来描述，参数 λ=10\lambda=10λ=10 ，有：
P(N(2)−N(1)≤5)=∑n=05e−1010nn!P(N(3)−N(2)=0)=e−10(10)00!=e−10\begin{array}{c} P(N(2)-N(1)\leq 5)=\sum\limits_{n=0}^{5}e^{-10}\frac{10^n}{n!} \\ P(N(3)-N(2)=0)=e^{-10}\frac{(10)^0}{0!}=e^{-10} \end{array} P(N(2)−N(1)≤5)=n=0∑5​e−10n!10n​P(N(3)−N(2)=0)=e−100!(10)0​=e−10​
小概率事件原理：实际当中有很多现象都可以用 Poisson 过程来描述，是因为 Bernoulli 实验的次数很多时，二项分布就会逼近 Poisson 分布。这些具体的性质用数学表述为：

Th：设 {N(t),t≥0}\{N(t),\,t\geq0\}{N(t),t≥0} 是一个计数过程，它满足：则它是一个 Poisson 过程

1. N(0)=0N(0)=0N(0)=0 ；
2. 过程有平稳独立增量
3. 存在 λ>0\lambda >0λ>0 ，当 h→0+h\to 0^+h→0+ 时，有：

P(N(t+h)−N(t)=1)=λh+o(h)P(N(t+h)-N(t)=1)=\lambda h+o(h) P(N(t+h)−N(t)=1)=λh+o(h)

4. 当 h→0+h\to 0^+h→0+ 时，有：

P(N(t+h)−N(t)≥2)=o(h)P(N(t+h)-N(t)\geq 2)=o(h) P(N(t+h)−N(t)≥2)=o(h)

大致说明：首先，我们把 [0,t][0,\,t][0,t] 划分为 nnn 个相等的区间，则由条件 4. 得到，当 n→∞n\to\inftyn→∞ 时，每个小区间内事件发生两次及以上的概率趋于 0，因此事件发生一次的概率 p≈λtnp\approx \lambda\frac{t}{n}p≈λnt​ （这里 tn\frac{t}{n}nt​ 大概就是上边条件中的 hhh ），事件不发生的概率 1−p≈1−λtn1-p\approx 1-\lambda\frac{t}{n}1−p≈1−λnt​ ，这恰好对应于 Bernoulli 的一次实验，而 N(t)N(t)N(t) 就相当于 nnn 重 Bernoulli 试验中成功的总次数。

严格证明：充分性：设计数过程 {N(t,t≥0}\{N(t,\,t\geq 0\}{N(t,t≥0} 满足以上四个条件，要证明它是 Poisson 过程，只需验证 N(t)N(t)N(t) 服从参数为 λt\lambda tλt 的 Poisson 分布。记：
Pn(t)=P(N(t)=n),n=0,1,2,⋯P(h)=P(N(h)≥1)=P1(h)+P2(h)+⋯=1−P0(h)\begin{align} P_n(t)=&\,P(N(t)=n),\quad n=0,\,1,\,2,\,\cdots \\ P(h)=&\,P(N(h)\geq 1) \\ =&\, P_1(h)+P_2(h)+\cdots \\ =&\,1-P_0(h) \end{align} Pn​(t)=P(h)===​P(N(t)=n),n=0,1,2,⋯P(N(h)≥1)P1​(h)+P2​(h)+⋯1−P0​(h)​​
则：
P0(t+h)=P(N(t+h)=0)=P(N(t+h)−N(t)=0,N(t)=0)=P(N(t+h)−N(t)=0)⋅P(N(t)=0)(独立增量性)=P0(t)P0(h)=P0(t)(1−λh+o(h))(条件3.)\begin{align} P_0(t+h)=&\,P(N(t+h)=0) \\ =&\,P(N(t+h)-N(t)=0,\,N(t)=0) \\ =&\,P(N(t+h)-N(t)=0)\cdot P(N(t)=0) \quad(独立增量性)\\ =&\,P_0(t)P_0(h) \\ =&\,P_0(t)(1-\lambda h+o(h))\quad (条件 3.) \end{align} P0​(t+h)=====​P(N(t+h)=0)P(N(t+h)−N(t)=0,N(t)=0)P(N(t+h)−N(t)=0)⋅P(N(t)=0)(独立增量性)P0​(t)P0​(h)P0​(t)(1−λh+o(h))(条件3.)​​
因此
P0(t+h)−P0(t)h=−λP0(t)+o(h)h\frac{P_0(t+h)-P_0(t)}{h}=-\lambda P_0(t)+\frac{o(h)}{h} hP0​(t+h)−P0​(t)​=−λP0​(t)+ho(h)​
令 h→0h\to 0h→0 ，得：
P0′(t)=−λP0(t)P_0'(t)=-\lambda P_0(t) P0′​(t)=−λP0​(t)
解这个微分方程，得到：
P0(t)=ce−λtP_0(t)=ce^{-\lambda t} P0​(t)=ce−λt
有初始条件 P0(0)=1P_0(0)=1P0​(0)=1 得 c=1c=1c=1 ，故：
P0(t)=e−λtP_0(t)=e^{-\lambda t} P0​(t)=e−λt
同理，当 n≥1n\geq 1n≥1 时，有：
Pn(t+h)=P(N(t+h)=n)=P(N(t+h)−N(t)=0)P(N(t)=n)+P(N(t+h)−N(t)=1)P(N(t)=n−1)+P(N(t+h)−N(t)≥2,N(t+h)=n)=P0(h)Pn(t)+P1(h)Pn−1(t)+o(h)=(1−λh)Pn(t)+λhPn−1(t)+o(h)\begin{align} P_n(t+h)=&\,P(N(t+h)=n) \\ =&\,P(N(t+h)-N(t)=0)P(N(t)=n)\\+&\,P(N(t+h)-N(t)=1)P(N(t)=n-1)\\+&\,P(N(t+h)-N(t)\geq 2,\,N(t+h)=n) \\ =&\,P_0(h)P_n(t)+P_1(h)P_{n-1}(t)+o(h) \\ =&\,(1-\lambda h)P_n(t)+\lambda hP_{n-1}(t)+o(h) \end{align} Pn​(t+h)==++==​P(N(t+h)=n)P(N(t+h)−N(t)=0)P(N(t)=n)P(N(t+h)−N(t)=1)P(N(t)=n−1)P(N(t+h)−N(t)≥2,N(t+h)=n)P0​(h)Pn​(t)+P1​(h)Pn−1​(t)+o(h)(1−λh)Pn​(t)+λhPn−1​(t)+o(h)​​
于是：
Pn(t+h)−Pn(t)h=−λPn(t)+λPn−1(t)+o(h)h\frac{P_n(t+h)-P_n(t)}{h}=-\lambda P_n(t)+\lambda P_{n-1}(t)+\frac{o(h)}{h} hPn​(t+h)−Pn​(t)​=−λPn​(t)+λPn−1​(t)+ho(h)​
令 h→0h\to 0h→0 ，解微分方程，代入初始条件，得到：
Pn(t)=e−λt(λt)nn!=P(N(t)=n)P_n(t)=e^{-\lambda t}\frac{(\lambda t)^n}{n!}=P(N(t)=n) Pn​(t)=e−λtn!(λt)n​=P(N(t)=n)
充分性：Poisson 过程已经满足条件 1. 和 2.，只需要证明满足条件 3. 和 4.，有：
P(N(t+h)−N(t)=1)=P(N(h)−N(0)=1)=e−λhλh1!=λh∑n−0∞(λh)nn!=λh(1−λh+o(h))(Taylor展开)=λh+o(h)\begin{align} P(N(t+h)-N(t)=1)=&\,P(N(h)-N(0)=1)\\ =&\,e^{-\lambda h}\frac{\lambda h}{1!}\\ =&\,\lambda h\sum\limits_{n- 0}^{\infty}\frac{(\lambda h)^n}{n!}=\lambda h(1-\lambda h+o(h))\quad(Taylor展开)\\=&\,\lambda h+o(h) \end{align} P(N(t+h)−N(t)=1)====​P(N(h)−N(0)=1)e−λh1!λh​λhn−0∑∞​n!(λh)n​=λh(1−λh+o(h))(Taylor展开)λh+o(h)​​

P(N(t+h)−N(t)≥2)=P(N(h)−N(0)≥2)=∑n=2∞e−λh(λh)nn!=o(h)\begin{align} P(N(t+h)-N(t)\geq 2)=&\,P(N(h)-N(0)\geq 2) \\ =&\, \sum\limits_{n=2}^{\infty}e^{-\lambda h}\frac{(\lambda h)^n}{n!} \\ =&\, o(h) \end{align} P(N(t+h)−N(t)≥2)===​P(N(h)−N(0)≥2)n=2∑∞​e−λhn!(λh)n​o(h)​​

很妙哇，我感觉就是泰勒展开的原理。

例：事件 AAA 的发生形成强度为 $\lambda $ 的 Poisson 过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} ，如果每次事件发生时能够以概率 ppp 被记录下来，并以 M(t)M(t)M(t) 表示到时刻 ttt 被记录下来的时间总数，则 {M(t),t≥0}\{M(t),\,t\geq 0\}{M(t),t≥0} 是一个强度为 λp\lambda pλp 的泊松过程

显然，M(t)M(t)M(t) 也一定有平稳独立增量，且 M(0)=0M(0)=0M(0)=0 ，只需要证明 M(t)M(t)M(t) 服从参数为 λp\lambda pλp 的 Poisson 过程
P(M(t)=m)=∑n=0∞P(M(t)=n∣N(t)=m+n)⋅P(N(t)=m+n)=∑n=0∞Cm+nmpm(1−p)n⋅e−λt(λt)m+n(m+n)!=1m!pm(λt)me−λt∑n=0∞(1−p)n(λt)nn!=1m!pm(λt)me−λte(1−p)λt=e−pλt(pλt)mm!\begin{align} P(M(t)=m)=&\,\sum\limits_{n=0}^{\infty}P(M(t)=n|N(t)=m+n)\cdot P(N(t)=m+n) \\ =&\, \sum\limits_{n=0}^{\infty}C_{m+n}^mp^m(1-p)^{n}\cdot e^{-\lambda t}\frac{(\lambda t)^{m+n}}{(m+n)!}\\ =&\,\frac{1}{m!}p^m(\lambda t)^me^{-\lambda t}\sum\limits_{n=0}^{\infty}\frac{(1-p)^n(\lambda t)^n}{n!} \\ =&\,\frac{1}{m!}p^m(\lambda t)^me^{-\lambda t}e^{(1-p)\lambda t} \\ =&\,e^{-p\lambda t}\frac{(p\lambda t)^m}{m!} \\ \end{align} P(M(t)=m)=====​n=0∑∞​P(M(t)=n∣N(t)=m+n)⋅P(N(t)=m+n)n=0∑∞​Cm+nm​pm(1−p)n⋅e−λt(m+n)!(λt)m+n​m!1​pm(λt)me−λtn=0∑∞​n!(1−p)n(λt)n​m!1​pm(λt)me−λte(1−p)λte−pλtm!(pλt)m​​​
故 M(t)M(t)M(t) 服从 λp\lambda pλp 的泊松过程

（这个例子相当于用一个泊松分布，以概率 ppp 导出得到了另一个泊松分布）

与 Poisson 过程相联系的若干分布

Poisson 的样本路径一般是跳跃度为 111 的阶梯函数：

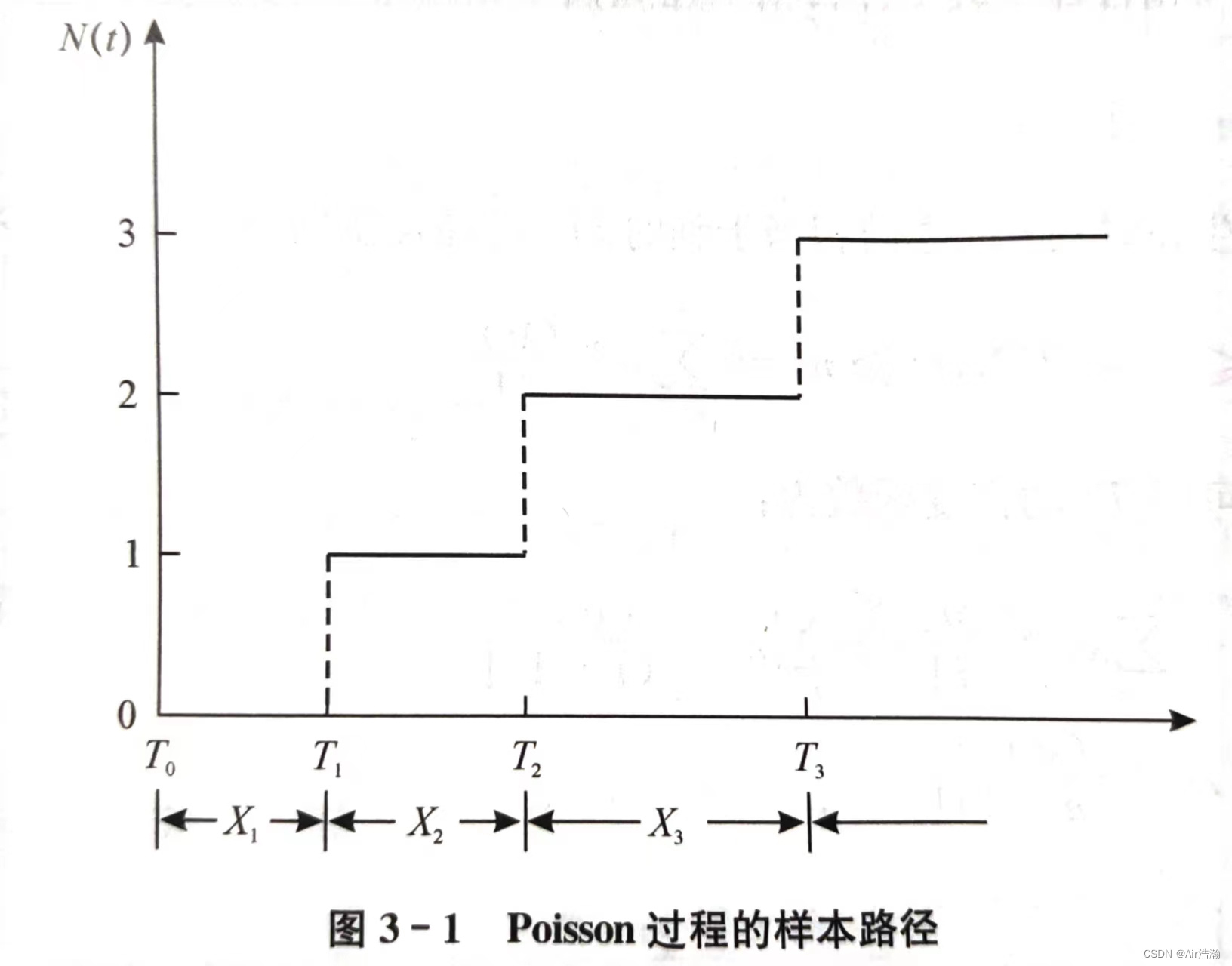
其中 TnT_nTn​ 代表第 nnn 次事件发生的间隔，规定 T0=0T_0=0T0​=0 ；XnX_nXn​ 代表第 nnn 次和第 n−1n-1n−1 次事件发生的时间间隔

XnX_nXn​ 和 TnT_nTn​ 的分布

XnX_nXn​ 的分布： XnX_nXn​ 服从参数为 λ\lambdaλ 的指数分布，且相互分布

证明：首先考虑 X1X_1X1​ 的分布，有：
P(X1>t)=P(N(t)=0)=e−λt⇒P(X1≤t)=1−e−λtP(X_1\gt t)=P(N(t)=0)=e^{-\lambda t}\Rightarrow P(X_1\leq t)=1-e^{-\lambda t} P(X1​>t)=P(N(t)=0)=e−λt⇒P(X1​≤t)=1−e−λt
再观察 X2X_2X2​ ，有：
P(X2>t∣X1=s)=P(N(t+s)−N(s)=0∣X1=s)=P(N(t+s)−N(s)=0)(独立增量性)=e−λt\begin{align} P(X_2\gt t|X_1=s)=&\,P(N(t+s)-N(s)=0|X_1=s) \\ =&\,P(N(t+s)-N(s)=0) \quad(独立增量性) \\ =&\, e^{-\lambda t} \end{align} P(X2​>t∣X1​=s)===​P(N(t+s)−N(s)=0∣X1​=s)P(N(t+s)−N(s)=0)(独立增量性)e−λt​​
所以 X1X_1X1​ 和 X2X_2X2​ 相互独立，且都服从参数为 λ\lambdaλ 的指数分布，可以重复推导

Def：Poisson 过程的第三种定义：计数过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 是参数为 λ\lambdaλ 的 Poisson 过程，如果每次事件的时间间隔 X1X_1X1​ ，X2X_2X2​ ，⋯\cdots⋯ 相互独立，且服从参数为 λ\lambdaλ 的指数分布。

（Poisson 过程具有平稳独立增量，正好对应于指数分布的无记忆性）

TnT_nTn​ 的分布：TnT_nTn​ 服从参数为 nnn 和 λ\lambdaλ 的 Γ\GammaΓ 分布

证明：由 Tn=∑i=1nXiT_n=\sum\limits_{i=1}^nX_iTn​=i=1∑n​Xi​ ，指数分布是参数为 111 和 λ\lambdaλ 的 Γ\GammaΓ 分布，由 Γ\GammaΓ 分布的独立可加性得到，TnT_nTn​ 服从参数为 nnn 和 λ\lambdaλ 的 Γ\GammaΓ 分布

例：设从早上 8：00 开始由无穷多人排队等候服务，只有一名服务员，且每个人接受服务的事件是独立的并服从均值为 20 分钟的指数分布，则到中午 12：00 为止平均有多少人已经离去？已有 9 个人接受服务的概率是多少？

由此可知离去的人数 {N(t)}\{N(t)\}{N(t)} 服从参数为 3 的泊松过程（以小时为单位），故：
P(N(4)−N(0)=n)=e−12(12)nn!P(N(4)-N(0)=n)=e^{-12}\frac{(12)^n}{n!} P(N(4)−N(0)=n)=e−12n!(12)n​
该分布的均值为 12，因此到中午 12：00 位置平均已有 12 人离去，已有 9 个人接受服务的概率为：P(N(4)−N(0)=9)=e−12(12)n9!P(N(4)-N(0)=9)=e^{-12}\frac{(12)^n}{9!}P(N(4)−N(0)=9)=e−129!(12)n​

事件发生各时刻的条件分布

假设到时刻 ttt ，Poisson 过程描述的事件 AAA 已经发生了 nnn 次，现在考虑 T1T_1T1​ ，T2T_2T2​ ，⋯\cdots⋯ TnT_nTn​ 的联合分布；首先考虑 n=1n=1n=1 的情况，对于 s≥ts\geq ts≥t ，有：
P(T1≤s∣N(t)=1)=P(T1≤s,N(t)=1)P(N(t)=1)=P(N(s)=1)⋅P(N(t)−N(s)=0)P(N(t)=1)=λse−λs⋅e−λ(t−s)λte−λt=st\begin{align} P(T_1\leq s|N(t)=1)=&\,\frac{P(T_1\leq s, N(t)=1)}{P(N(t)=1)} \\ =&\, \frac{P(N(s)=1)\cdot P(N(t)-N(s)=0)}{P(N(t)=1)} \\ =&\, \frac{\lambda se^{-\lambda s}\cdot e^{-\lambda(t-s)}}{\lambda te^{-\lambda t}} \\ =&\, \frac{s}{t} \end{align} P(T1​≤s∣N(t)=1)====​P(N(t)=1)P(T1​≤s,N(t)=1)​P(N(t)=1)P(N(s)=1)⋅P(N(t)−N(s)=0)​λte−λtλse−λs⋅e−λ(t−s)​ts​​​
可以理解成，在已知 [0,t][0,\,t][0,t] 时间内 AAA 只发生一次的前提下，AAA 发生时刻在 [0,t][0,\,t][0,t] 上是均匀分布的，这是因为 Poisson 过程具有平稳独立增量，AAA 在 [0,t][0,\,t][0,t] 的任何长度相同的子区间内发生的概率都是相等的。现在考虑 n≥2n\geq 2n≥2 的情况：

Th：在已知 N(t)=nN(t)=nN(t)=n 的条件下，事件发生的 nnn 个时刻 T1T_1T1​ ，T2T_2T2​ ，⋯\cdots⋯ TnT_nTn​ 的联合概率密度函数为：
f(t1,t2,⋯,tn)=n!tn,0 证明：设 0 P(ti

按照定义，给定 N(t)=nN(t)=nN(t)=n 时，(T1,T2,⋯Tn)(T_1,\,T_2,\,\cdots\,T_n)(T1​,T2​,⋯Tn​) 的 nnn 为条件分布密度为：
f(t1,t2,⋯,tn)=lim⁡hi→0P(ti 这个式子恰好是 [0,t][0,\,t][0,t] 区间上服从均匀分布的 nnn 个相互独立随机变量 Y1Y_1Y1​ ，Y2Y_2Y2​ ，⋯\cdots⋯ ，YnY_nYn​ 的顺序统计量 Y(1)Y_{(1)}Y(1)​ ，Y(2)Y_{(2)}Y(2)​ ，⋯\cdots⋯ ，Y(n)Y_{(n)}Y(n)​ 的联合分布。所以直观上，在已知 [0,t][0,\,t][0,t] 内发生了 nnn 次事件的前提下，各事件发生的时刻 T1T_1T1​ ，T2T_2T2​ ，⋯\cdots⋯ ，TnT_nTn​ （不排序）可看作相互独立的随机变量，且都服从 [0,t][0,\,t][0,t] 上的均匀分布。

例：乘客按照强度为 λ\lambdaλ 的 Poisson 过程来到某火车站，火车在 ttt 时刻启程，计算在 (0,t](0,\,t](0,t] 内到达的乘客等待事件的总和的期望值，即求 E[∑i=1N(t)(t−Ti)]E\left[ \sum\limits_{i=1}^{N(t)}(t-T_i) \right]E[i=1∑N(t)​(t−Ti​)] ，其中 TiT_iTi​ 是第 iii 个乘客到达的时刻

解：在 N(t)N(t)N(t) 给定的条件下，取条件期望：
E[∑i=1N(t)(t−Ti)∣N(t)=n]=E[∑i=1n(t−Ti)∣N(t)=n]=nt−E[∑i=1nTi∣N(t)=n]E\left[ \sum\limits_{i=1}^{N(t)}(t-T_i)|N(t)=n \right]=E\left[ \sum\limits_{i=1}^n(t-T_i)|N(t)=n \right]=nt-E\left[ \sum\limits_{i=1}^nT_i|N(t)=n \right] E​i=1∑N(t)​(t−Ti​)∣N(t)=n​=E[i=1∑n​(t−Ti​)∣N(t)=n]=nt−E[i=1∑n​Ti​∣N(t)=n]
由上边证明的定理得， nnn 个乘客的到来可以看作 nnn 个服从均匀分布的随机变量，记 U1U_1U1​ ，U2U_2U2​ ，⋯\cdots⋯ ，UnU_nUn​ 为 nnn 个独立的服从 (0,t](0,\,t](0,t] 上均匀分布的随机变量，有：
E[∑i=1nTi∣N(t)=n]=E(∑i=1nUi)=nt2E\left[ \sum\limits_{i=1}^nT_i|N(t)=n \right]=E(\sum\limits_{i=1}^nU_i)=\frac{nt}{2} E[i=1∑n​Ti​∣N(t)=n]=E(i=1∑n​Ui​)=2nt​
因此：
E[∑i=1N(t)(t−Ti)∣N(t)=n]=nt−E[∑i=1nTi∣N(t)=n]=nt2E\left[ \sum\limits_{i=1}^{N(t)}(t-T_i)|N(t)=n \right]=nt-E\left[ \sum\limits_{i=1}^nT_i|N(t)=n \right]=\frac{nt}{2} E​i=1∑N(t)​(t−Ti​)∣N(t)=n​=nt−E[i=1∑n​Ti​∣N(t)=n]=2nt​
所以：
E[∑i=1N(t)(t−Ti)]=E{E[∑i=1N(t)(t−Ti)∣N(t)]}=∑n=0∞nt2⋅P(N(t)=n)=λt22E\left[ \sum\limits_{i=1}^{N(t)}(t-T_i) \right]=E\left\{ E\left[ \sum\limits_{i=1}^{N(t)}(t-T_i)|N(t) \right] \right\}=\sum\limits_{n=0}^{\infty}\frac{nt}{2}\cdot P(N(t)=n)=\frac{\lambda t^2}{2} E​i=1∑N(t)​(t−Ti​)​=E⎩⎨⎧​E​i=1∑N(t)​(t−Ti​)∣N(t)​⎭⎬⎫​=n=0∑∞​2nt​⋅P(N(t)=n)=2λt2​
（我猜条件期望就是这样算的吧hhh）

Poisson 过程的推广

非齐次 Poisson 过程

非齐次 Poisson 过程：Poisson 过程中的 λ\lambdaλ 不再是常数，二而是与时间 ttt 有关的函数时，就推广成了非齐次 Poissson 过程。定义为：计数过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 称作强度函数为 λ(t)\lambda(t)λ(t) （λ(t)>0,t≥0\lambda(t)\gt 0,\,t\geq 0λ(t)>0,t≥0） 的非齐次 Poisson 过程，如果：

• N(0)=0N(0)=0N(0)=0 ；
• {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 具有独立增量；
• P(N(t+h)−N(t)=1)=λ(t)h+o(h)P(N(t+h)-N(t)=1)=\lambda(t)h+o(h)P(N(t+h)−N(t)=1)=λ(t)h+o(h) ；
• P(N(t+h)−N(t)≥2)=o(h)P(N(t+h)-N(t)\geq 2)=o(h)P(N(t+h)−N(t)≥2)=o(h) ；

若令 m(t)=∫0tλ(s)dsm(t)=\int_{0}^t\lambda(s)\,dsm(t)=∫0t​λ(s)ds ，则类似于 Poisson 过程；非齐次 Poisson 过程有如下等价定义：

Def：计数过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 称为强度函数为 λ(t)\lambda(t)λ(t) （λ(t)>0,t≥0\lambda(t)\gt 0,\,t\geq 0λ(t)>0,t≥0） 的非齐次 Poisson 过程，如果：

• N(0)=0N(0)=0N(0)=0 ；
• {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 具有独立增量；
• 对任意实数 t≥0t\geq 0t≥0 ，s>0s\gt 0s>0 ，N(t+s)−N(t)N(t+s)-N(t)N(t+s)−N(t) 为具有参数 m(t+s)−m(t)=∫tt+sλ(u)dum(t+s)-m(t)=\int_{t}^{t+s}\lambda(u)\,dum(t+s)−m(t)=∫tt+s​λ(u)du 的 Poisson 分布

此时称 m(t)m(t)m(t) 为非齐次 Poisson 过程的均值函数（或累计强度函数）

非齐次 Poisson 过程的重要性在于不再要求平稳增量性，从而允许时间在某些时刻发生的可能性比另外一些时刻大。

以下定理给出了 Poisson 过程与非齐次 Poisson 过程之间的转换关系；事实上，非齐次 Poisson 过程就是进行时间变换过后的 Poisson 过程，使得某些时候时间更密，某些时候时间更稀疏，于是 λ\lambdaλ 就变得随着时间变化了。

Th：设{N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 是强度函数为 λ(t)\lambda(t)λ(t) 的非齐次 Poisson 过程。对任意 t≥0t\geq 0t≥0 ，令 N∗(t)=N[m−1(t)]N^*(t)=N[m^{-1}(t)]N∗(t)=N[m−1(t)] ，则 {N∗(t)}\{N^*(t)\}{N∗(t)} 是一个强度为 1 的 Poisson 过程。

（很显然 m(t)=∫0tλ(s)dsm(t)=\int_{0}^t\lambda(s)\,dsm(t)=∫0t​λ(s)ds 是一个单调递增函数，所以有反函数）

证明：我们证明 N∗(t)N^*(t)N∗(t) 满足第一节中 Poisson 过程的第二个定义。由 N(t)N(t)N(t) 的性质，易得 N∗(t)N^*(t)N∗(t) 满足条件 1. 和 2. ，我们只需证明其满足条件 3. 和 4. ；

记 v(t)=m−1(t)v(t)=m^{-1}(t)v(t)=m−1(t) ，则 N∗(t)=N[v(t)]N^*(t)=N[v(t)]N∗(t)=N[v(t)] ；设 v=m−1(t)v=m^{-1}(t)v=m−1(t) ，v+h′=m−1(t+h)v+h'=m^{-1}(t+h)v+h′=m−1(t+h) ，则：
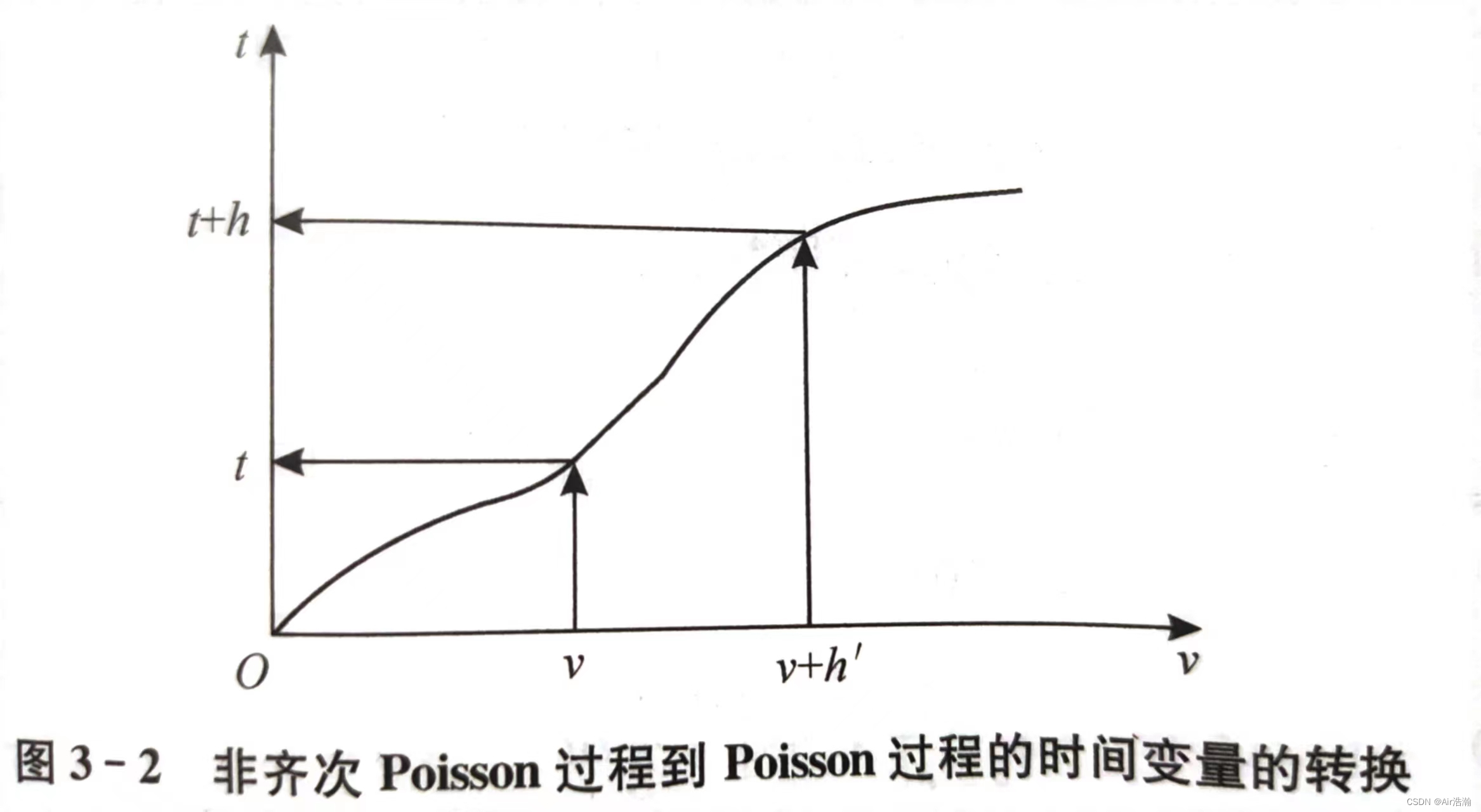
h=m(v+h′)−m(v)=∫vv+h′λ(s)ds=λ(v)h′+o(h′)h=m(v+h')-m(v)=\int_{v}^{v+h'}\lambda(s)\,ds=\lambda(v)h'+o(h') h=m(v+h′)−m(v)=∫vv+h′​λ(s)ds=λ(v)h′+o(h′)
（这一步我没有太懂，我觉得是这样：假设 λ(t)\lambda(t)λ(t) 连续（一般都是这样），由积分中值定理得 ∫vv+h′λ(s)ds=h′λ(v+ε)\int_{v}^{v+h'}\lambda(s)\,ds=h'\lambda(v+\varepsilon)∫vv+h′​λ(s)ds=h′λ(v+ε)，其中 0≤ε≤h′0\le \varepsilon \leq h'0≤ε≤h′ ，而 λ(v+ε)=λ(v)+o(1)\lambda(v+\varepsilon)=\lambda(v)+o(1)λ(v+ε)=λ(v)+o(1) （在 vvv 处泰勒展开），因此 =h′λ(v)+o(h′)=h'\lambda(v)+o(h')=h′λ(v)+o(h′) ）

得：
lim⁡h→0+P(N∗(t+h)−N∗(t)=1)h=lim⁡h→0+P(N(v+h′)−N(v)=1)λ(v)h′+o(h′)(上边推导出来的h=λ(v)h′+o(h′))=lim⁡h→0+λ(v)h′+o(h′)λ(v)h′+o(h′)=1(非齐次Poisson过程的定义中的第3个条件)\begin{align} &\,\lim_{h\to 0^+}\frac{P(N^*(t+h)-N^*(t)=1)}{h} \\ =&\,\lim_{h\to 0^+}\frac{P(N(v+h')-N(v)=1)}{\lambda(v)h'+o(h')} \quad(上边推导出来的\,h=\lambda(v)h'+o(h'))\\ =&\,\lim_{h\to 0^+}\frac{\lambda(v)h'+o(h')}{\lambda(v)h'+o(h')}=1 \quad(非齐次Poisson过程的定义中的第3个条件) \end{align} ==​h→0+lim​hP(N∗(t+h)−N∗(t)=1)​h→0+lim​λ(v)h′+o(h′)P(N(v+h′)−N(v)=1)​(上边推导出来的h=λ(v)h′+o(h′))h→0+lim​λ(v)h′+o(h′)λ(v)h′+o(h′)​=1(非齐次Poisson过程的定义中的第3个条件)​​
即：（条件 3. ）
P(N∗(t+h)−N∗(t)=1)=h+o(h)P(N^*(t+h)-N^*(t)=1)=h+o(h) P(N∗(t+h)−N∗(t)=1)=h+o(h)
同理可得：
lim⁡h→0+P(N∗(t+h)−N∗(t)≥2)h=lim⁡h→0+P(N(v+h′)−N(v)≥2)λ(v)h′+o(h′)(上边推导出来的h=λ(v)h′+o(h′))=lim⁡h→0+o(h′)λ(v)h′+o(h′)=0(非齐次Poisson过程的定义中的第4个条件)\begin{align} &\,\lim_{h\to 0^+}\frac{P(N^*(t+h)-N^*(t)\geq 2)}{h} \\ =&\,\lim_{h\to 0^+}\frac{P(N(v+h')-N(v)\geq 2)}{\lambda(v)h'+o(h')} \quad(上边推导出来的\,h=\lambda(v)h'+o(h'))\\ =&\,\lim_{h\to 0^+}\frac{o(h')}{\lambda(v)h'+o(h')}=0 \quad(非齐次Poisson过程的定义中的第4个条件) \end{align} ==​h→0+lim​hP(N∗(t+h)−N∗(t)≥2)​h→0+lim​λ(v)h′+o(h′)P(N(v+h′)−N(v)≥2)​(上边推导出来的h=λ(v)h′+o(h′))h→0+lim​λ(v)h′+o(h′)o(h′)​=0(非齐次Poisson过程的定义中的第4个条件)​​
即：（条件 4. ）
P(N∗(t+h)−N∗(t)≥2=o(h)P(N^*(t+h)-N^*(t)\geq 2=o(h) P(N∗(t+h)−N∗(t)≥2=o(h)
所以 {N∗(t),t≥0}\{N^*(t),\,t\geq 0\}{N∗(t),t≥0} 是参数为 111 的 Poisson 过程

注意：可以用这个定理将非齐次 Poisson 过程的问题简化到 Poisson 过程中进行讨论，也可以反过来操作

例：设某设备的使用期限为 10 年，前 5 年内它平均 2.5 年需要维修一次，后 5 年平均两年需要维修一次，试求他在试用期内只维修过一次的概率。

标准解答：考虑为非齐次 Poisson 过程，强度函数：
λ(t)={12.50≤t≤51252.51​21​​0≤t≤55 则：
m(10)=∫010λ(s)ds=∫0512.5ds+∫51012ds=4.5m(10)=\int_{0}^{10}\lambda(s)\,ds=\int_{0}^{5}\frac{1}{2.5}\,ds+\int_{5}^{10}\frac{1}{2}\,ds=4.5 m(10)=∫010​λ(s)ds=∫05​2.51​ds+∫510​21​ds=4.5
因此：
P(N(10)−N(0))=1=e−4.54.511!=92e−92P(N(10)-N(0))=1=e^{-4.5}\frac{4.5^1}{1!}=\frac{9}{2}e^{-\frac{9}{2}} P(N(10)−N(0))=1=e−4.51!4.51​=29​e−29​
我的解答：就像上面解释的，将非齐次 Poisson 过程看作时间伸缩过后的 Poisson 过程。前 5 年平均 2.5 年需要维修一次，可以看成 4 年内平均每 2 年需要维修一次，这样 λ\lambdaλ 就统一为了 12\frac{1}{2}21​ ，此时 n=4+5=9n=4+5=9n=4+5=9 ，故 P(N(t)=1)=e−12⋅9(12⋅9)11!=92e−92P(N(t)=1)=e^{-\frac{1}{2}\cdot 9}\frac{(\frac{1}{2}\cdot9)^1}{1!}=\frac{9}{2}e^{-\frac{9}{2}}P(N(t)=1)=e−21​⋅91!(21​⋅9)1​=29​e−29​

复合 Poisson 过程

复合 Poisson 过程：称随机过程 {X(t),t≥0}\{X(t),\,t\geq 0\}{X(t),t≥0} 为复合 Poisson 过程，如果对于 t≥0t\ge 0t≥0 ，它可以表示为：
X(t)=∑i=1N(t)YiX(t)=\sum\limits_{i=1}^{N(t)}Y_i X(t)=i=1∑N(t)​Yi​
式中，{N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 是一个 Poisson 过程，{Yi,i=1,2,⋯}\{Y_i,\,i=1,\,2,\,\cdots\}{Yi​,i=1,2,⋯} 是一族独立同分布的随机变量，并且与 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 独立

复合 Poisson 过程不一定是计数过程，但是当 Yi≡cY_i\equiv cYi​≡c 时，可以转化为 Poisson 过程

例：保险公司每年需要被索赔的人数服从泊松分布，但是每个人需要赔偿的金额是个随机的随机变量；走进商店的顾客人数是个泊松过程，但是每个人消费的金额是个随机的随机变量；这些都可以用复合 Poisson 过程表示。

Th：设 {X(t)=∑i=1N(t)Yi,t≥0}\left\{ X(t)=\sum\limits_{i=1}^{N(t)}Y_i,\,t\geq 0 \right\}{X(t)=i=1∑N(t)​Yi​,t≥0} 是一个复合泊松过程，其中泊松过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 的强度为 λ\lambdaλ ，则：

• X(t)X(t)X(t) 有独立增量；
• 若 E(Yi2)<∞E(Y_i^2)\lt \inftyE(Yi2​)<∞ ，则 E[X(t)]=λtE(Y1)E[X(t)]=\lambda tE(Y_1)E[X(t)]=λtE(Y1​) ，Var[X(t)]=λtE(Y12)Var[X(t)]=\lambda tE(Y_1^2)Var[X(t)]=λtE(Y12​) ；

证明我没有看懂，跳过吧hhh；注意这里 YiY_iYi​ 是独立同分布的，所以选择 Y1Y_1Y1​ 还是 YiY_iYi​ 作为 E(X)E(X)E(X) 和 Var(X)Var(X)Var(X) 的表达式都没u关系

例：设顾客以每分钟 6 人的平均速率进入商场，进入商场的每位顾客买东西的概率为 0.9 ，且顾客是否消费与商场人数无关、相互独立，求商城一天（按 12 小时计）中消费的顾客数的均值。

解：这里套了一层的复合 Poisson 过程，以 N1(t)N_1(t)N1​(t) 表示在时间 (0,t](0,\,t](0,t] 内进入商场的顾客数（单位为分钟），则 {N1(t),t≥0}\{N_1(t),\,t\geq 0\}{N1​(t),t≥0} 是速率为 λ=6\lambda=6λ=6 的 Poisson 过程。再以 N2(t)N_2(t)N2​(t) 表示在时间 (0,t](0,\,t](0,t] 内在该商场消费的顾客数，并设：
Yi={1如果第i位顾客消费了0如果第i位顾客没消费Y_i=\left\{ \begin{array}{ll} 1 & 如果第\,i\,位顾客消费了 \\ 0 & 如果第\,i\,位顾客没消费 \\ \end{array} \right. Yi​={10​如果第i位顾客消费了如果第i位顾客没消费​
则 YiY_iYi​ 独立同分布与 B(1,0.9)B(1,\,0.9)B(1,0.9) ，与 {N1(t),t≥0}\{N_1(t),\,t\geq 0\}{N1​(t),t≥0} 独立，且：
N2(t)=∑i=1N1(t)YiN_2(t)=\sum\limits_{i=1}^{N_1(t)}Y_i N2​(t)=i=1∑N1​(t)​Yi​
所以商城一天中消费的顾客数的均值为 E[N2(720)]=3888E[N_2(720)]=3888E[N2​(720)]=3888 人；

条件 Poisson 过程

条件 Poisson 过程：涉及具体个体时，λ\lambdaλ 可能是固定的，但是不同个体的 λ\lambdaλ 又是不同的。我们可以把分布式解释为给定 λ\lambdaλ 时，N(t)N(t)N(t) 的条件分布 PN∣λ(t)P_{N|\lambda}(t)PN∣λ​(t) ，数学定义为：设随机变量 Λ>0\Lambda \gt 0Λ>0 ，在 Λ=λ\Lambda=\lambdaΛ=λ 的条件下，计数过程 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 是参数为 λ\lambdaλ 的 Poisson 过程，则称 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 为条件 Poisson 过程。

设 Λ\LambdaΛ 的分布为 GGG ，那么随机选择一个个体在长度为 ttt 的时间区间内发生 nnn 次事件的概率为：
P(N(t+s)−N(s)=n)=∫0∞e−λt(λt)nn!dG(λ)P(N(t+s)-N(s)=n)=\int_0^\infty e^{-\lambda t}\frac{(\lambda t)^n}{n!}\,dG(\lambda) P(N(t+s)−N(s)=n)=∫0∞​e−λtn!(λt)n​dG(λ)
这里 {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 不是 Poisson 过程，它只具有平稳增量，而不具有独立增量

Th： {N(t),t≥0}\{N(t),\,t\geq 0\}{N(t),t≥0} 为条件 Poisson 过程，且 E(Λ2)<∞E(\Lambda^2)<\inftyE(Λ2)<∞ ，则：

1. E[N(t)]=tE(Λ)E[N(t)]=tE(\Lambda)E[N(t)]=tE(Λ) ；
2. Var[N(t)]=t2Var(Λ)+tE(Λ)Var[N(t)]=t^2Var(\Lambda)+tE(\Lambda)Var[N(t)]=t2Var(Λ)+tE(Λ) ；

证明：
E[N(t)]=E[E(N(t)∣Λ)]=∑λE(N(t)∣λ)⋅P(Λ=λ)=tE(Λ)\begin{align} E[N(t)]=&\,E[E(N(t)|\Lambda)] \\ =&\,\sum\limits_{\lambda}E(N(t)|\lambda)\cdot P(\Lambda=\lambda) \\ =&\,tE(\Lambda) \end{align} E[N(t)]===​E[E(N(t)∣Λ)]λ∑​E(N(t)∣λ)⋅P(Λ=λ)tE(Λ)​​

Var[N(t)]=E[N2(t)]−[E(N(t))]2=∑λE(N2(t)∣λ)⋅P(Λ=λ)−t2E2(Λ)=∑λ(λt+λ2t2)⋅P(Λ=λ)−t2E2(Λ)\begin{align} Var[N(t)]=&\,E[N^2(t)]-[E(N(t))]^2 \\ =&\,\sum\limits_{\lambda}E(N^2(t)|\lambda)\cdot P(\Lambda=\lambda)-t^2E^2(\Lambda) \\ =&\,\sum\limits_{\lambda}(\lambda t+\lambda^2t^2)\cdot P(\Lambda=\lambda)-t^2E^2(\Lambda) \\ \end{align} Var[N(t)]===​E[N2(t)]−[E(N(t))]2λ∑​E(N2(t)∣λ)⋅P(Λ=λ)−t2E2(Λ)λ∑​(λt+λ2t2)⋅P(Λ=λ)−t2E2(Λ)​​

我真的不会条件期望的求法。。。按照我自己的理解来做：
Var(Λ)=E(Λ2)−E2(Λ)=∑λλ2P(Λ=λ)−E2(Λ)⇒∑λλ2P(Λ=λ)=Var(Λ)+E2(Λ)Var(\Lambda)=E(\Lambda^2)-E^2(\Lambda)=\sum\limits_{\lambda}\lambda^2P(\Lambda=\lambda)-E^2(\Lambda)\Rightarrow \sum\limits_{\lambda}\lambda^2P(\Lambda=\lambda)=Var(\Lambda)+E^2(\Lambda) Var(Λ)=E(Λ2)−E2(Λ)=λ∑​λ2P(Λ=λ)−E2(Λ)⇒λ∑​λ2P(Λ=λ)=Var(Λ)+E2(Λ)
因此：
Var[N(t)]=t∑λλ⋅P(Λ=λ)+t2∑λλ2P(Λ=λ)−t2E2(Λ)=tE(Λ)+t2(Var(λ)+E2(Λ))−t2E2(Λ)=t2Var(Λ)+tE(Λ)\begin{align} Var[N(t)]=&\,t\sum\limits_{\lambda}\lambda \cdot P(\Lambda=\lambda)+t^2\sum\limits_{\lambda}\lambda^2P(\Lambda=\lambda)-t^2E^2(\Lambda) \\ =&\,tE(\Lambda)+t^2(Var(\lambda)+E^2(\Lambda))-t^2E^2(\Lambda) \\ =&\,t^2Var(\Lambda)+tE(\Lambda) \end{align} Var[N(t)]===​tλ∑​λ⋅P(Λ=λ)+t2λ∑​λ2P(Λ=λ)−t2E2(Λ)tE(Λ)+t2(Var(λ)+E2(Λ))−t2E2(Λ)t2Var(Λ)+tE(Λ)​​
例：（这个例子属实是硬造出来的）设意外事故的发生频率受某种未知因素影响有两种可能 λ1\lambda_1λ1​ 和 λ2\lambda_2λ2​ ，且 P(Λ=λ1)=pP(\Lambda=\lambda_1)=pP(Λ=λ1​)=p ，P(Λ=λ2)=1−p=qP(\Lambda=\lambda_2)=1-p=qP(Λ=λ2​)=1−p=q ，0

下一次事故在 t+st+st+s 之前不会到来的概率，就是在已知到了时刻 ttt 发生了 nnn 次事故的条件下，N(t+s)−N(t)N(t+s)-N(t)N(t+s)−N(t) 为 0 的概率，为：
∑i=12P(N(t)=n,N(s+t)−N(t)=0∣Λ=λi)∑i=12P(N(t)=n∣Λ=λ1)P(Λ=λi)=pλ1ne−λ1(t+s)+qλ2ne−λ2(t+s)pλ1ne−λ1t+qλ2ne−λ2t\frac{\sum\limits_{i=1}^2P(N(t)=n,\,N(s+t)-N(t)=0|\Lambda=\lambda_i)}{\sum\limits_{i=1}^2P(N(t)=n|\Lambda=\lambda_1)P(\Lambda=\lambda_i)}=\frac{p\lambda_1^ne^{-\lambda_1(t+s)}+q\lambda_2^ne^{-\lambda_2(t+s)}}{p\lambda_1^ne^{-\lambda_1t}+q\lambda_2^ne^{-\lambda_2t}} i=1∑2​P(N(t)=n∣Λ=λ1​)P(Λ=λi​)i=1∑2​P(N(t)=n,N(s+t)−N(t)=0∣Λ=λi​)​=pλ1n​e−λ1​t+qλ2n​e−λ2​tpλ1n​e−λ1​(t+s)+qλ2n​e−λ2​(t+s)​
以及：（贝叶斯公式，这里的分母已经在上边的式子里求出来了）
P(Λ=λ1∣N(t)=n)=P(Λ=λ1,N(t)=n)P(N(t)=n∣Λ=λ1)+P(N(t)=n∣Λ=λ2)=pλ1ne−λ1tpλ1ne−λ1t+qλ2ne−λ2tP(\Lambda=\lambda_1|N(t)=n)=\frac{P(\Lambda=\lambda_1,\,N(t)=n)}{P(N(t)=n|\Lambda=\lambda_1)+P(N(t)=n|\Lambda=\lambda_2)}=\frac{p\lambda_1^ne^{-\lambda_1t}}{p\lambda_1^ne^{-\lambda_1t}+q\lambda_2^ne^{-\lambda_2t}} P(Λ=λ1​∣N(t)=n)=P(N(t)=n∣Λ=λ1​)+P(N(t)=n∣Λ=λ2​)P(Λ=λ1​,N(t)=n)​=pλ1n​e−λ1​t+qλ2n​e−λ2​tpλ1n​e−λ1​t​