数据结构第一二章笔记
仅仅是自己学习记的一些笔记。
1.一些零碎的知识
时间复杂度:
找出哪一条语句执行的次数最多
他的执行次数就是时间复杂度
O(n^3)


空间复杂度:
当局部变量只有固定几个值的时候他们的空间复杂度为O(1),该算法为原地工作算法。
n->∞
根号n的大于log2n
2.1线性表
线性表的基本概念
2.1.1线性表的定义
线性表是由n(n>=0)个相同类型的数据元素组成的有限序列。
标记:List(线性表)
L(List)=(a1,a2,a3 ……,ai……,an)
线性表中元素的个数n定义为线性表的长度,当n=0时为空表。
当n>0时,线性表的逻辑表结构图:一个接一个

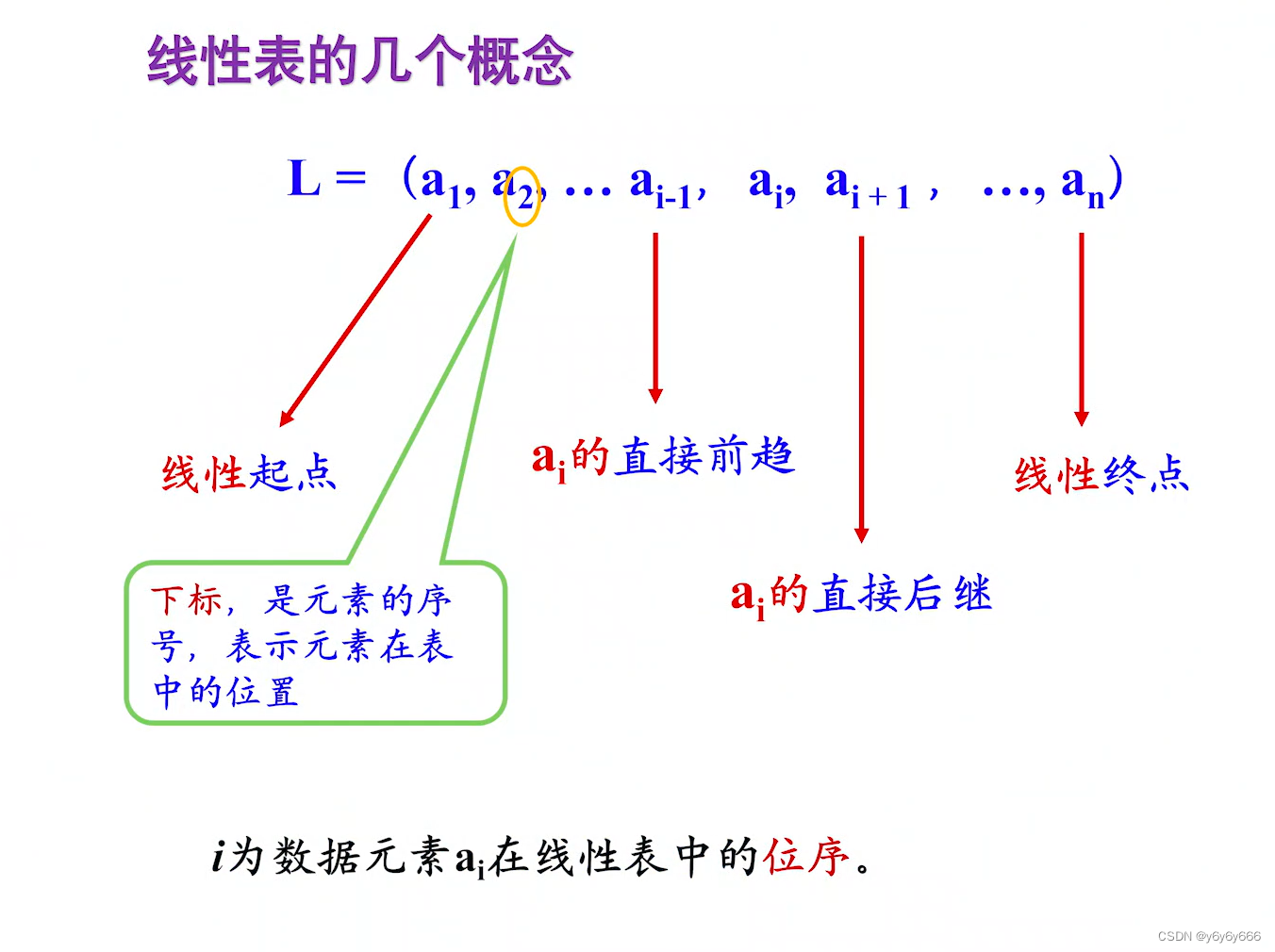
*i为数据元素ai在线性表中的位序。
逻辑特征:
若至少含有一个元素,则只唯一的起始元素;
若至少含有一个元素,则只有唯一的尾元素。
除了起始元素外,其他元素有且仅有一个前驱元素。
除了尾节点外,其他元素有且仅有一个后继元素。
线性表中的每个元素有唯一的序号(逻辑序号),同一个线性表中可以存在值相同的多个元素。
但他们的序号是不同的。
2.1.2线性表的基本运算
初始化InitList(L)。建立一个空表L(即建立线性表的架构,但是不含任何元素)
销毁线性表DestroyList(L).
其作用是释放线性表L的内存空间。
求线性表的长度ListLength(L)
其作用是返回线性表L的长度。
求线性表中第i个元素。
GetElem(L,i,e)
其作用是返回线性表L的第i个数据元素。
按值查找LocateElem(L,x).
若L中存在一个或多个值与x相等的元素,则其作用是返回第一个值为x的元素的序列号。
*插入元素,ListInsert(L,i,x)
作用是在线性表L的第i,个位置上增加一个以x为值的新元素
*删除元素ListDelete(L,i)
删除第i个位置的元素ai
输出元素值DispList(L)
其作用是按照前后顺序输出线性表L的所有元素值。
线性表抽象数据类型List:
ADT LIST {
线性表中元素逻辑结构;
基本运算定义;
}
开头是0
loc(i)=loc(i-1)+l=a+i*l
或
开头是1
loc(i)=a+(i-1)*l
假定线性表元素的元素类型为ElemType,
//线性表的动态分配顺序存储结构---
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分量
#define LIST_INCREMENT 10 //线性表存储空间的分配增量
typedef int ElemType; //元素的数据类型
typedef struct{ElemType *elem; //存储空间(基地址)首地址int length; //当前长度int listsize; //当前分配的存储容量
}SqList;//线性表的静态分配顺序存储结构---
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分量
typedef int ElemType; //元素的数据类型
typedef struct{ElemType data[MaxSize]; //存储空间(基地址)首地址int length; //当前长度
}SqList; //顺序表类型实际上静态用的多,一旦空间使用完不可扩充
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
typedef int Status;//Status值是函数结果状态代码顺序存储具有随机存储的特性。
2.2.2顺序表基本运算的实现
(1)初始化线性表算法
将顺序表L的length域置为0
Status InitList_Sq(SqList &L)
{
//算法2.3构造一个空的线性表·L
L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(!L.elem)return ERROR;//空间分配失败
L.length=0; //空表长度
L.listsize=LIST_INIT_SIZE;//初始储存容量
return OK;
}(2)销毁线性表
由于顺序表的内存空间是由动态分配得到的,在不再需要时应该主动释放其空间。
Status DestroyList(SqList &L)
{//初始条件:顺序线性表L已存在。操作结果销毁顺序线性表Lfree(L.elem);L.elem=NULL;L.length=0;L.listsize=0;return OK;
}(3)求线性表的返回长度运算算法
返回顺序表L的length阈值
int GetLength(SqList L)
{return L.length;
}(4)求线性表中第i个元素算法·
在位序(逻辑序号)无效时返回特殊值0(假),
有效时返回1真,并用引用型形参e返回第i个元素的值·。
Status GetElem(SqList L,int i,ElemType &e)
{//初始条件:线性表已经在,1<=i<=ListLength(L)
//操作结果:用e返回L中第i个数据元素的值
if(i<1||i>L.leth)return ERROR;
e=*(L.elem+i-1);
return OK;
}(5)按值查找算法
在顺序表L找第一个值为e的元素,找到后返回其逻辑序号,否则返回0(由于线性表的逻辑序号从1开始这里用0表示没有找到e的元素)。
int LocateElem(SqList L,ElemType e)
{ElemType *p;int i=1; //i的初值为第i个元素的位序
p=L.elem; //p的初值为第i个元素的储存位置
while(i<=L.length&&(*p++!=e))
++i;
if(i<=L.length)
return i;
else return 0;(6)插入算法·Insert
将新元素e插入到顺序表L中逻辑序号为i的位置(如 果插入成功,元素e成为线性表的第i个元素)。 i的合法值为1≤i≤L.Length+1。当i无效时返回0(表 示插入失败)。 有效时将L.elem[i-1..L.length-1]后移一个位置, 在L.elem[i-1]处插入e,顺序表长度增1,并返回1 (表示插入成功)。
Status ListInsert_Sq(SqList &L, int i, ElemType e)
{ // 算法2.4; i的合法值为1≤i≤L.Length+1
ElemType *p;
if(i < 1 || i > L.length + 1)
return ERROR; // i值不合法
if(L.length >= L.listsize) { // 当前存储空间已满,增加容量
ElemType *newbase = (ElemType *)realloc(L.elem,
(L.listsize + LISTINCREMENT) * sizeof(ElemType));
if(!newbase)
return ERROR; // 存储分配失败
L.elem = newbase; // 新基址
L.listsize += LISTINCREMENT; // 增加存储容量
}
ElemType *q = &(L.elem[i - 1]); // q为插入位置
for(p = &(L.elem[L.length - 1]); p >= q; --p)
*(p + 1) = *p; // 插入位置及之后的元素右移
*q = e; // 插入e
++L.length; // 表长增1
return OK;
} 时间复杂度O(n)
(7)删除算法Delete
删除顺序表L中逻辑序号为i的元素
Status ListDelete_Sq(SqList &L, int i, ElemType &e)
{ // 算法2.5; i的合法值为1≤i≤ListLength_Sq(L)。
ElemType *p, *q;
if(i < 1 || i > L.length)
return ERROR; // i值不合法
p = &(L.elem[i - 1]); // p为被删除元素的位置
e = *p; // 被删除元素的值赋给e
q = L.elem + L.length - 1; // 表尾元素的位置
for(++p; p <= q; ++p)
*(p - 1) = *p; // 被删除元素之后的元素左移
--L.length; // 表长减1
return OK;
}算法分析:
当i=n时(删除尾元素),移动次数为0,最好的情况。
i=1时,移动i-1次,最坏
时间复杂度O(n)
3、c语言指针实现
// #include
// using namespace std;
#include
#include // 线性表的动态分配顺序存储结构---
#define LIST_INIT_SIZE 100 // 线性表存储空间的初始分量
#define LIST_INCREMENT 10 // 线性表存储空间的分配增量
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MaxSize 100
typedef int Status; // Status值是函数结果状态代码
typedef int ElemType; // 元素的数据类型
typedef struct
{ElemType *elem; // 存储空间(基地址)首地址int length; // 当前长度int listsize; // 当前分配的存储容量
} SqList;Status InitList_Sq(SqList* L);
int GetLength(SqList* L);
Status ListInsert_Sq(SqList *L, int i, ElemType e);
Status GetElem(SqList *L, int i, ElemType *e);
int LocateElem(SqList* L, ElemType e);
Status ListDelete_Sq(SqList *L, int i, ElemType* e);
Status DestroyList(SqList* L);
void main()
{SqList L;InitList_Sq(&L);printf("长度%d\n", GetLength(&L));int i = 1, e = 6;ListInsert_Sq(&L, i, e);printf("插入后外部%d\n", GetLength(&L));int e2=0; //e2用来存储返回的元素。//线性表中第i个元素GetElem(&L, i, &e2);printf("e2=%d\n",e2);int i2=e; //查找i2的位置printf("i2下标%d\n",LocateElem(&L,i2));int e3;ListDelete_Sq(&L,i, &e3);printf("e3==%d\n",e3);DestroyList(&L);printf("销毁后长度%d\n", GetLength(&L));}/*
// 线性表的静态分配顺序存储结构---
#define LIST_INIT_SIZE 100 // 线性表存储空间的初始分量
typedef int ElemType; // 元素的数据类型
typedef struct
{ElemType data[MaxSize]; // 存储空间(基地址)首地址int length; // 当前长度
} SqList; // 顺序表类型
*/// 初始化
Status InitList_Sq(SqList* L)
{// 算法2.3构造一个空的线性表·LL->elem = (ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType));if (!L->elem)return ERROR; // 空间分配失败L->length= 0; // 空表长度L->listsize = LIST_INIT_SIZE; // 初始储存容量return OK;
}// 销毁线性表
Status DestroyList(SqList* L)
{ // 初始条件:顺序线性表L已存在。操作结果销毁顺序线性表Lfree(L->elem);L->elem = NULL;L->length = 0;L->listsize = 0;return OK;
}// 求线性表的长度
int GetLength(SqList* L)
{return L->length;
}// 求线性表中第i个元素
Status GetElem(SqList *L, int i, ElemType *e)
{ // 初始条件:线性表已经在,1<=i<=ListLength(L)// 操作结果:用e返回L中第i个数据元素的值if (i < 1 || i > L->length)return ERROR;*e = *(L->elem + i - 1);//printf("函数内部%d",*e);return OK;
}// 按照值查找
int LocateElem(SqList* L, ElemType e)
{ElemType *p;int i = 1; // i的初值为第i个元素的位序p = L->elem; // p的初值为第i个元素的储存位置while (i <= L->length && (*p++!= e))++i;if (i <= L->length)return i;elsereturn 0;
}
// 插入算法(将e插入到下标为i的位置)
Status ListInsert_Sq(SqList* L, int i, ElemType e)
{ // 算法2.4; i的合法值为1≤i≤L.Length+1ElemType *p;if (i < 1 || i > L->length + 1){return ERROR; // i值不合法}if (L->length >= L->listsize){ // 当前存储空间已满,增加容量ElemType *newbase = (ElemType *)realloc(L->elem,(L->listsize + LIST_INCREMENT) * sizeof(ElemType));if (!newbase)return ERROR; // 存储分配失败L->elem = newbase; // 新基址L->listsize += LIST_INCREMENT; // 增加存储容量}ElemType *q = &(L->elem[i - 1]); // q为插入位置for (p = &(L->elem[L->length - 1]); p >= q; --p){*(p + 1) = *p; // 插入位置及之后的元素右移}*q = e; // 插入e++(L->length); // 表长增1return OK;
}//(7)删除算法,删除顺序表L中逻辑序号为i的元素
Status ListDelete_Sq(SqList* L, int i, ElemType* e)
{ // 算法2.5; i的合法值为1≤i≤ListLength_Sq(L)。ElemType *p, *q;if (i < 1 || i > L->length)return ERROR; // i值不合法p = &(L->elem[i - 1]); // p为被删除元素的位置*e = *p; // 被删除元素的值赋给eq = L->elem + L->length - 1; // 表尾元素的位置for (++p; p <= q; ++p)*(p - 1) = *p; // 被删除元素之后的元素左移--L->length; // 表长减1return OK;
} 4.c++引用类型实现
#include
#include
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MaxSize 100
typedef int Status; // Status值是函数结果状态代码// // 线性表的静态分配顺序存储结构---
// #define LIST_INIT_SIZE 100 // 线性表存储空间的初始分量
// typedef int ElemType; // 元素的数据类型
// typedef struct
// {
// ElemType data[MaxSize]; // 存储空间(基地址)首地址
// int length; // 当前长度
// } SqList; // 顺序表类型// 线性表的动态分配顺序存储结构---
#define LIST_INIT_SIZE 100 // 线性表存储空间的初始分量
#define LIST_INCREMENT 10 // 线性表存储空间的分配增量
typedef int ElemType; // 元素的数据类型
typedef struct
{ElemType *elem; // 存储空间(基地址)首地址int length; // 当前长度int listsize; // 当前分配的存储容量
} SqList;
Status InitList_Sq(SqList &L);
int GetLength(SqList L);
Status GetElem(SqList L, int i, ElemType &e);
int LocateElem(SqList L, ElemType e);
Status ListInsert_Sq(SqList &L, int i, ElemType e);
Status ListDelete_Sq(SqList &L, int i, ElemType &e);
Status DestroyList(SqList &L);int main()
{SqList L;InitList_Sq(L);printf("插入前长度%d\n",GetLength(L));ListInsert_Sq(L,1,6);printf("插入后长度%d\n",GetLength(L));//返回第i个元素的值给eint e;GetElem(L,1,e);printf("第一个元素的值%d\n",e);printf("6的下标是%d\n",LocateElem(L,6));int d;ListDelete_Sq(L, 1, d);printf("删除的元素的值是%d\n",d);DestroyList(L);printf("销毁后长度%d\n",GetLength(L));return 0;
}Status InitList_Sq(SqList &L)
{// 算法2.3构造一个空的线性表·LL.elem = (ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType));if (!L.elem)return ERROR; // 空间分配失败L.length = 0; // 空表长度L.listsize = LIST_INIT_SIZE; // 初始储存容量return OK;
}int GetLength(SqList L)
{return L.length;
}Status GetElem(SqList L, int i, ElemType &e)
{ // 初始条件:线性表已经在,1<=i<=ListLength(L)// 操作结果:用e返回L中第i个数据元素的值if (i < 1 || i > L.length)return ERROR;e = *(L.elem + i - 1);return OK;
}int LocateElem(SqList L, ElemType e)
{ElemType *p;int i = 1; // i的初值为第i个元素的位序p = L.elem; // p的初值为第i个元素的储存位置while (i <= L.length && (*p++ != e))++i;if (i <= L.length)return i;elsereturn 0;
}
Status ListInsert_Sq(SqList &L, int i, ElemType e)
{ // 算法2.4; i的合法值为1≤i≤L.Length+1ElemType *p;if (i < 1 || i > L.length + 1)return ERROR; // i值不合法if (L.length >= L.listsize){ // 当前存储空间已满,增加容量ElemType *newbase = (ElemType *)realloc(L.elem,(L.listsize + LIST_INCREMENT) * sizeof(ElemType));if (!newbase)return ERROR; // 存储分配失败L.elem = newbase; // 新基址L.listsize += LIST_INCREMENT; // 增加存储容量}ElemType *q = &(L.elem[i - 1]); // q为插入位置for (p = &(L.elem[L.length - 1]); p >= q; --p)*(p + 1) = *p; // 插入位置及之后的元素右移*q = e; // 插入e++L.length; // 表长增1return OK;
}
//删除第i个元素
Status ListDelete_Sq(SqList &L, int i, ElemType &e)
{ // 算法2.5; i的合法值为1≤i≤ListLength_Sq(L)。ElemType *p, *q;if (i < 1 || i > L.length)return ERROR; // i值不合法p = &(L.elem[i - 1]); // p为被删除元素的位置e = *p; // 被删除元素的值赋给eq = L.elem + L.length - 1; // 表尾元素的位置for (++p; p <= q; ++p)*(p - 1) = *p; // 被删除元素之后的元素左移--L.length; // 表长减1return OK;
}Status DestroyList(SqList &L)
{ // 初始条件:顺序线性表L已存在。操作结果销毁顺序线性表Lfree(L.elem);L.elem = NULL;L.length = 0;L.listsize = 0;return OK;
} 5.线性表题目(c++)
// #include
#include
#include
// 线性表的动态分配顺序存储结构---
#define LIST_INIT_SIZE 100 // 线性表存储空间的初始分量
#define LIST_INCREMENT 10 // 线性表存储空间的分配增量
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MaxSize 100
typedef int Status; // Status值是函数结果状态代码
typedef int ElemType; // 元素的数据类型typedef struct
{ElemType *elem; // 存储空间(基地址)首地址int length; // 当前长度int listsize; // 当前分配的存储容量
} SqList;
void dispList(SqList L);
Status InitList_Sq(SqList &L);
Status ListInsert_Sq(SqList &L, int i, ElemType e);
Status ListDelete_Sq(SqList &L, int i, ElemType &e);
void SwapMaxMin(SqList &L);
void swap(ElemType &x, ElemType &y);
int Deletek(SqList &L, int i, int k);int main()
{int A[8] = {1, 2, 3, 4, 5, 100, 200, 300};int i, j, e = 586;SqList List;InitList_Sq(List);for (i = 1, j = 0; i <= 8; i++, j++)ListInsert_Sq(List, i, A[j]);printf("\n插入之前的元素序列为:\n");dispList(List);i = 3;ListInsert_Sq(List, i, e);printf("\n\n插入后的元素序列为:\n");dispList(List);i = 6; // 删除位置printf("\n\n删除后的元素序列:\n");ListDelete_Sq(List, i, e);dispList(List);SwapMaxMin(List);printf("\n\n交换后的元素序列:\n");dispList(List);Deletek(List, 1, 3);printf("删除三个后\n");dispList(List);return 0;
}
// 查看线性表
void dispList(SqList L)
{for (int i = 1; i <= L.length; i++){printf("%d ", L.elem[i - 1]);}
}// 初始化线性表
Status InitList_Sq(SqList &L)
{L.elem = (ElemType *)malloc(LIST_INIT_SIZE * sizeof(ElemType));if (!L.elem)return ERROR; // 如果头指针是空,表示分配失败L.length = 0; // 长度L.listsize = LIST_INIT_SIZE; // 大小return OK;
}// 插入
Status ListInsert_Sq(SqList &L, int i, ElemType e)
{ElemType *p;if (i < 1 || i > L.length + 1)return ERROR;if (L.length > L.listsize){ElemType *newbase = (ElemType *)realloc(L.elem, (L.listsize + LIST_INCREMENT) * sizeof(ElemType));if (!newbase)return ERROR; // 添加空间失败L.elem = newbase; // 新基址L.listsize += LIST_INCREMENT; // 添加容量}ElemType *q = &(L.elem[i - 1]); // q为插入位置for (p = &(L.elem[L.length - 1]); p >= q; --p) // 判断条件是p>=q*(p + 1) = *p; // 插入位置及之后的元素后移*q = e; // 插入e++L.length; // 长度加1return OK;
}
// 删除第i个元素
Status ListDelete_Sq(SqList &L, int i, ElemType &e)
{ElemType *p, *q;if (i < 1 || i > L.length)return ERROR; // i值不合法p = &(L.elem[i - 1]); // p为被删除元素的位置e = *p; // 被删除元素的值赋给eq = L.elem + L.length - 1; // 表尾元素的位置for (++p; p <= q; ++p)*(p - 1) = *p; // 被删除元素之后的元素左移--L.length; // 表长减1return OK;
}// 假设有一个顺序表L,其中元素为整数且
// 所有元素值均不相同。设计一个算法将最大值元素与最
// 小值元素交换。
// 用maxi和mini记录顺序表L中最大值元素和最小值
// 元素的下标,初始时maxi=mini=0。
// i从1开始扫描所有元素:当
// L.elem[i]>L.elem[maxi]时置maxi=i;否则若
// L.elem[i] L.elem[maxi]){maxi = i;}else if (L.elem[i] < L.elem[mini])mini = i;swap(L.elem[maxi], L.elem[mini]);
}// 设计一个算法,从线性表中删除自第i个元
// 素开始的k个元素,其中线性表用顺序表L存储。
//
// 算法思路将线性表中ai
// ~ai+k-1元素(对应L.elem[i-1..i+k-2]的
// 元素)删除,即将ai+k
// ~an(对应L.elem[i+k-1..n-1])
// 的所有元素依次前移k个位置int Deletek(SqList &L, int i, int k)
{int j;if (i < 1 || k < 1 || i + k - 1 > L.length)return 0; // 判断i和k是否合法for (j = i + k - 1; j < L.length; j++) // 将元素前移k个位置{L.elem[j - k] = L.elem[j];}L.length -= k; // L的长度减kreturn 1;
}// 已知线性表(a1,a2,…,an)采用顺序表L存
// 储,且每个元素都是互不相等的整数。设计一个将所有
// 奇数移到所有的偶数前边的算法(要求时间最少,辅助
// 空间最少)
// 算法思路
// 算法设计思路:置i=0,j=n-1,在顺序表L中从左向右
// 找到偶数L.elem[i],从右向左找到奇数L.elem[j],将两
// 者交换;循环这个过程直到i等于j为止。void Move(SqList &L)
{int i = 0, j = L.length - 1;while (i < j){while (L.elem[i] % 2 == 1)i++; // 从前向后找偶数while (L.elem[j] % 2 == 0)j--; // 从后向前找奇数if (i < j)swap(L.elem[i], L.elem[j]); // 交换这两元素}
}// 已知一个整数线性表采用顺序表L存储。
// 设计一个尽可能高效的算法删除其中所有值为负整数的
// 元素(假设L中值为负整数的元素可能有多个)
// 采用整体重建顺序表的算法思路,仅仅将插入元素
// 的条件设置为“元素值≥0”即可。void DeleteMinus(SqList &L)
{int i, k = 0;for (i = 0; i < L.length; i++)if (L.elem[i] >= 0) // 将不为负数的元素插入到L中{L.elem[k] = L.elem[i];k++;}L.length = k; // 重置L的长度
}
