文法的形式定义
一、序列的集合称为形式语言
序列的集合称为形式语言
二、形式语言的描述
当语言是有穷集合时,用枚举法表示。
EX:
设字母表A={a,b,c},则
L1={a,b,c}
L2={a,aa,bb,ac}
L3={c,cc}
均表示字母表A上的一个形式语言。
2.当语言是无穷集合时,用文法来描述(文法实际上时一组规律)
EX:
Σ={0,1},则Σ+={0,1,00,,01,10,11,000,001,……}

上例可表示为:A->0 A->1 A->A0 A->A1
反复用这个例子,不计较其顺序,反复用则产生:Σ+={0,1,00,01,10,000,001,……}
文法作用:是用有穷集合描述无穷集合的一种工具
三、文法的形式定义
文法的直观认识
语言应该包括语法和语义两个方面。
语法用来定义什么样的符号序列是合法的,与这些法号的含义毫无关系
EX:
狗是小狗
文法是用来形式化定义语法的工具。
文法的定义:是定义规则的非空有穷集合。定义为:
G=(VT,VN,S,P)是一个四元组,
其中
VT:终结符的集合,可出现在文法的任何地方;
VN:非终结符的集合;且有VT∩VN=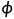
规则(产生式)
是一个符号与一个符号串的有序对(偶),(A,a),通常写作A->α,通常写作(A->α)
或者(A::α)
①、一个规则作用:描述语言中句子是怎样产生的;
②、一组规则作用:描述一个语言的语法结构。
非终结符:能推导/导出/派出 符号、符号串(一般在左部)
终结符:不能派生出符号串的符号(不可再分的单位)
S:文法的开始符号 P:文法规则式的集合
EX:
A->0 VT={0,1}
A->1 VN={A}
A->A0 S=A
A-->A1 P : A->0|1|A0|A1
EX:
设Σ={a,b},试设计一个文法,定义语言L: L={ a^2n ,b^2n |n>=1 }
分析:看一下这个语言里句子结构的特征(串结构的特征)
L={aa,bb,aaaa,bbbb,aaaaaa,bbbbbb,……}
即L中有偶数个a,偶数个b,
则文法为:
P1:
A->aa VT={a,b}
A->aaB VN={A,B,D}
B->aa | aaB S:A
A->bb G={VT,VN,S,P}
A->bbD
D->bb|bbD
从上式子可以看出来:
①描述语言的文法是不唯一的;
②用文法描述语言要准确的描述,既不能扩大,也不能缩小。
EX:
用文法定义一个含 +,* 的算术表达式,定义用下述自然语言描述:变量是一个表达式;若E1和E2是算术表达式,则E1+E2,E1*E2,(E1)也是算术表达式。
形式化描述:
P:
E->i;
E->E + E | E*E | (E)
相当于 L={i,i+i,(i),i+i*i,……}
EX:
设计一个表示所有标识符的文法。
分析:标识符为以字母开头的字母数字串即:
字母|字母开头 字母数字串
P: I ->L | ID | IL
L->a|b|……|z|A|B|……|Z
D->0|1|2|……9
P: I->L | ID
L->a|b|……|z|A|B|……|Z
D->0|1|2|3|4……9
下边的文法产生式中只能生成字母在前,数字在后的串,不能生成如a1b1这样的串,故此文法将其功能缩小了
EX:已知语言L={(n)^n | n=0,1,2,3,……},试求L对应的文法G
解: L={ ,(),(()),((())),……}
,(),(()),((())),……}
P: S-> |(S)
|(S)
