【蓝桥杯】背包问题--DP动态规划入门
创始人
2025-05-30 12:36:48

解题思路:

DP动态规划的思路就是：

在有 K 件物品（每个物品都有自己的重量与价值，记为w[i]、v[i]）、背包容量为 W 时可以获取的最大价值，对于这种情况可以记为 f（K,W），值为可以获取的最大价值

在这种情况下有两种方式可以求解：

第一种就是：不拿第 K 件物品，在 1-（K-1）的范围内挑选物品，此时问题变为：在 K-1 件物品、背包容量为 W 时可以获取的最大价值，记为f（K-1,W）;

第二种就是：拿第 K 件物品，此时背包容量为 W-（第 K 件物品所占的重量），已获取的价值为（第 n 件物品所具有的的价值），此时的问题变为在 n-1 件物品、

背包容量为 W-w[K] 时可以获取的最大价值,记为 f（K-1,W-W[K]）+ V[K]；

原问题的解就是两种情况中价值较大的那一个；

注意事项:

1.可以列出一个矩阵来记录所有状态下的解，val【i】【j】,i 用来枚举出 n 件物品，j 用来枚举背包容量

2.要列出状态转移方程，该题的状态转移方程为：

3.以题中例子为例：

有三个物品，背包容量为5；

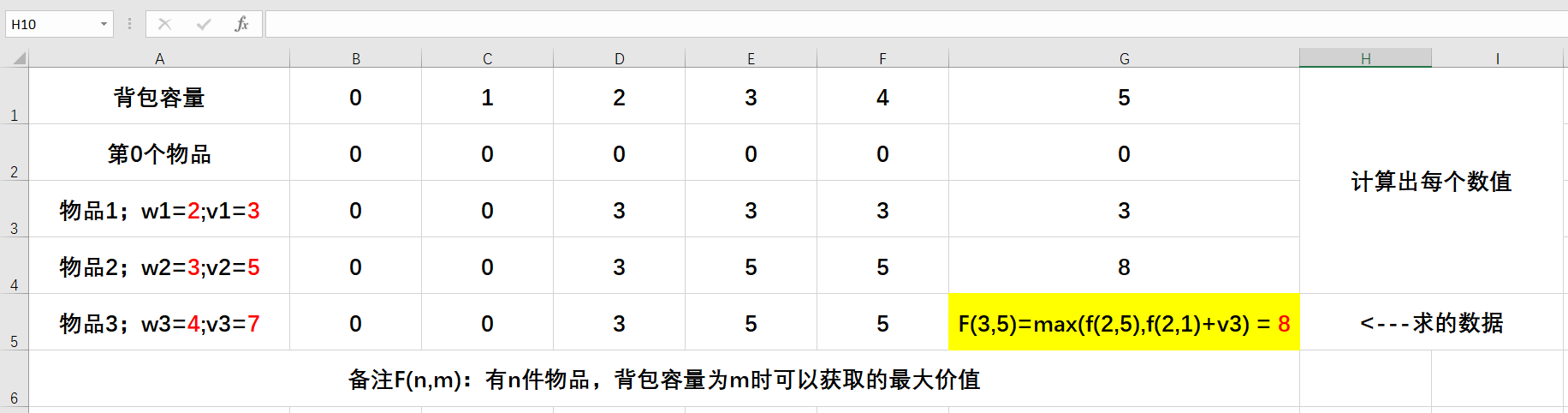
参考代码:

//简单背包问题 
#include 
using namespace std;
const int maxn = 200; 
const int maxm = 5000;  //最多可以装5000重量的东西
int val[maxn+10][maxm+10];   //表示当前状态可以装的最大值，【物品个数】【背包容量】 
int w[maxn+10];  //存储物品的重量 
int v[maxn+10];  //存储物品的价值 
int main(){memset(val,0,sizeof(val));int n,m;cin>>n>>m;int ww,vv; //存储每个物品的数据    [0][i]与[i][0]都是0，一个代表可以拿0个物品，一个是还有0个剩余重量 for(int i=1;i<=n;++i){cin>>ww>>vv;w[i]=ww;v[i]=vv;}//开始处理for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){if(w[i]>j)   //j表示可以拿多大重量的物品val[i][j] = val[i-1][j];elseval[i][j] = max(val[i-1][j],val[i-1][j-w[i]]+v[i]); }} cout<

视频参考链接（讲的真不错）

动态规划DP0-1背包_哔哩哔哩_bilibili

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：【代码随想录-刷题学习JavaScript】day1-part01数组

下一篇：春运什么时候可以订票?2023春节车票什么时候开始订（春运什么时候购票） 1月7号开始春运什么时候提前买票 春运2023订票时间

相关内容

热门资讯

电子拣货标签3代系统简介 CK_Label_v3 一、产品参数  1. 电池供电版 产品型号 CK_Label_v3 尺...
2023新车上牌费用是多少?上... 今天给各位分享2023新车上牌费用是多少?上牌照需要多少钱的知识，其中也会对2022年上牌进行解释，...
荣事达竟然是美的集团旗下品牌?... 今天给各位分享荣事达竟然是美的集团旗下品牌?!的知识，其中也会对荣事达美的合并了吗进行解释，如果能碰...
火车站次查询（火车站查询车次）... 本篇文章极速百科给大家谈谈火车站次查询，以及火车站查询车次对应的知识点，希望对各位有所帮助，不要忘了...
分集水器的详细使用方法,学会供... 本篇文章极速百科给大家谈谈分集水器的详细使用方法,学会供暖不会再有办法，以及分集水器构造详图对应的知...
c++ error:cross... 最近在写代码的时候，碰到了 crosses initialization of ......
机器学习模型的性能评估方法 动动发财的小手，点个赞吧！ 部署模型后，监控其性能对于确保...
俄罗斯土地面积多少平方公里（世... 本篇文章极速百科给大家谈谈俄罗斯土地面积多少平方公里，以及世界领土最大的三个国家对应的知识点，希望对...
ysl83是什么颜色 极速百科... ysl83是什么颜色目录ysl83是什么颜色ysl83是什么颜色圣罗兰纯魅唇膏86号适合黄皮女生素颜...
信用贷款怎么申请,个人信用贷款... 信用贷款怎么申请目录信用贷款怎么申请个人信用贷款怎么贷如何办理个人信用贷款？个人信用贷款怎么贷信用贷...
泾县有哪些景点,泾县十大必去景... 泾县有哪些景点目录泾县有哪些景点泾县十大必去景点泾县旅游景点泾县景点泾县有哪些景点 泾县位于安...
Leveraging Sali... Leveraging Saliency in Single-Stage Multi-Label Co...
ES-数据建模 数据模型是描述现实世界某种现象或者状态的物理抽象，比如我们之前用FSA来描述周老师的一...
进击的巨人大结局,进击的巨人漫... 进击的巨人大结局目录进击的巨人大结局进击的巨人漫画最终结局漫画《进击的巨人》大结局是什么？进击的巨人...
免单活动是什么意思 极速百科网... 免单活动是什么意思目录免单活动是什么意思免单活动是什么意思告诉我，免单是什么意思免单活动是什么意思免...
meld是手机里的什么,mel... meld是什么意思? meld是什么意思?作为全球唯一的标识，作用相当于我们每个人的。扩展资料：查找...
中华什么多奇志（中华什么多奇志... 本篇文章极速百科给大家谈谈中华什么多奇志，以及中华什么多奇志不爱红装爱武装英文对应的知识点，希望对各...
Linux C++实现进程间通... 基本知识 基本知识介绍参考：https://mp.weixin.qq.com/s/oS...
2023年ACM竞赛班 202...  目录 瞎编乱造第一题 瞎编乱造第二题 瞎编乱造第三题 瞎编乱造第四题 瞎编乱造第五题 不是很想编了...
windows安装包管理工具C... Chocolatey介绍Chocolatey 通过使用通用打包格式来管理 Windows 软件的各个...
解决：centos7如何解决网... 遇到此类问题可能会有多重解决方法，需要一个一个的去排除。 1、查看自己的网络设置是不是...
百克特1103是什么意思,请问... 百克特1103是什么意思目录百克特1103是什么意思请问，白克特1101和1103是什么病毒扫地机器...
无话不谈彼此陪伴什么意思,无话... 无话不谈彼此陪伴什么意思目录无话不谈彼此陪伴什么意思无话不谈是什么意思无话可说和无话不谈有什么区别？...
58同城企业认证的注册号是什么... 58同城企业认证的注册号是什么目录58同城企业认证的注册号是什么企业认证里的人注册号是什么我在58同...
草字头的字（草字头的字和什么有... 本篇文章极速百科给大家谈谈草字头的字，以及草字头的字和什么有关一年级对应的知识点，希望对各位有所帮助...
CentOS8提高篇2：Cen... 一、下载安装包 到wps官网下载linux版本的安装包， 根据自己的linux是 32...
这款开源管理文档管理系统兼容P... demo软件园每日更新资源,请看到最后就能获取你想要的: 1.《计算机网络实验教程》课后答案   ...
SpringBoot学习笔记(... 测试 加载测试专用属性 在启动测试环境时可以通过properties参数设置测试环境专用的属性 &#...
东方明珠什么时候开灯,东方明珠... 东方明珠什么时候开灯目录东方明珠什么时候开灯东方明珠几点开灯东方明珠几点亮灯？东方明珠几点开灯东方明...
一亩等于几分地一分地多少平方,... 一亩等于几分地一分地多少平方目录一亩等于几分地一分地多少平方一亩几分地?一分几个平方一分地多少平方一...