1题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

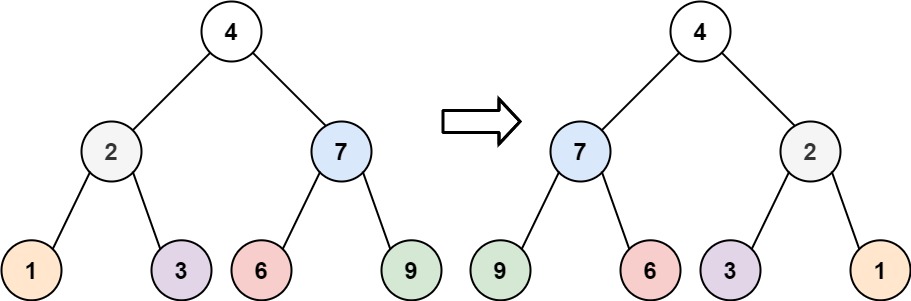
输入：root = [4,2,7,1,3,6,9]

输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]

输出：[2,3,1]

示例 3：

输入：root = []

输出：[]

2链接

题目：226. 翻转二叉树 - 力扣（Leetcode）

视频：听说一位巨佬面Google被拒了，因为没写出翻转二叉树 | LeetCode：226.翻转二叉树_哔哩哔哩_bilibili

3解题思路

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！

3.1递归法

以前序遍历为例，通过动画来看一下翻转的过程:

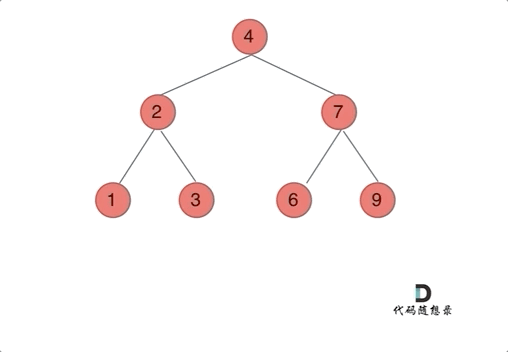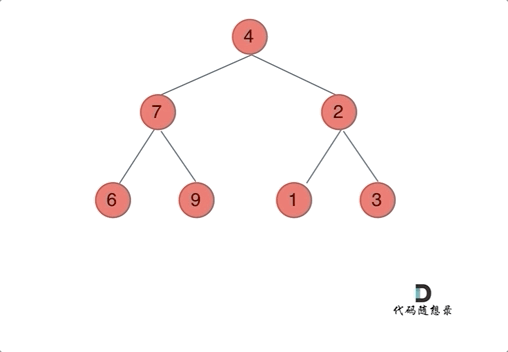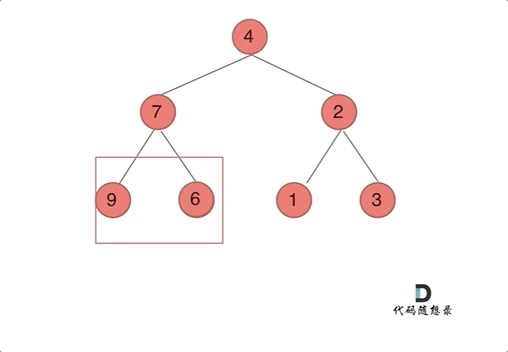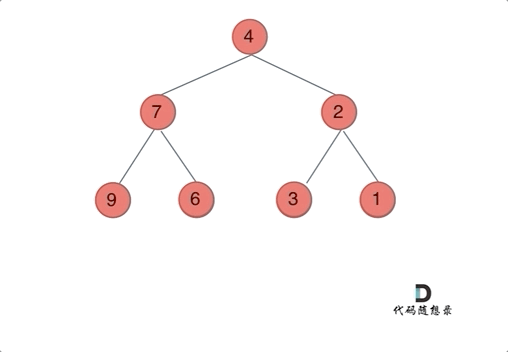
1. 确定递归函数的参数和返回值

参数就是要传入节点的指针，不需要其他参数了，通常此时定下来主要参数，如果在写递归的逻辑中发现还需要其他参数的时候，随时补充。

返回值的话其实也不需要，但是题目中给出的要返回root节点的指针，可以直接使用题目定义好的函数，所以就函数的返回类型为TreeNode*。

TreeNode*invertTree(TreeNode* root)

2. 确定终止条件

当前节点为空的时候，就返回

if(root ==NULL)return root;

3. 确定单层递归的逻辑

因为是先前序遍历，所以先进行交换左右孩子节点，然后反转左子树，反转右子树

swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);

3.2中序遍历递归法

如果非要使用递归中序的方式写，也可以，如下代码就可以避免节点左右孩子翻转两次的情况：

class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;invertTree(root->left);         // 左swap(root->left, root->right);  // 中invertTree(root->left);         // 注意 这里依然要遍历左孩子，因为中间节点已经翻转了return root;}
};

代码虽然可以，但这毕竟不是真正的递归中序遍历了。

但使用迭代方式统一写法的中序是可以的。

代码如下：

class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right);  // 右st.push(node);                          // 中st.push(NULL);if (node->left) st.push(node->left);    // 左} else {st.pop();node = st.top();st.pop();swap(node->left, node->right);          // 节点处理逻辑}}return root;}
};

3.2迭代法

3.3.1深度优先遍历

以前序遍历为例，氛围普通写法和统一写法两种，将会在后续代码中体现

3.3.2广度优先遍历

也就是层序遍历，层数遍历也是可以翻转这棵树的，因为层序遍历也可以把每个节点的左右孩子都翻转一遍

4代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///递归
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == nullptr) return root;swap(root -> left, root -> right);//中invertTree(root -> left);//左invertTree(root -> right);//右return root;}
};// 迭代法（前序遍历）-深度优先遍历
class Solution{
public:TreeNode* invertTree(TreeNode* root) {if (root == nullptr) return root;stack st;st.push(root);while (!st.empty()) {TreeNode* node = st.top();//中st.pop();swap(node -> left, node -> right);if (node -> right) st.push(node -> right);//右if (node -> left) st.push(node -> left);//左}return root;}
};//迭代法（统一写法前序遍历）-深度优先遍历
class Solution{
public:TreeNode* invertTree(TreeNode* root) {stack st;if (root == nullptr) return root;st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != nullptr) {st.pop();if (node -> right) st.push(node -> right);if (node -> left) st.push(node -> left);st.push(node);st.push(nullptr);}else {st.pop();//先弹出去nullptrnode = st.top();st.pop();//弹出节点swap(node -> left, node -> right); //交换左右孩子}}return root;}
};//迭代法-广度优先遍历
class Solution{
public:TreeNode* invertTree(TreeNode* root) {queue que;if (root == nullptr) return root;que.push(root);while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();swap(node->left, node->right);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return root;}
};