A.构造

• 一、问题
• 二、分析
• 三、代码

一、问题

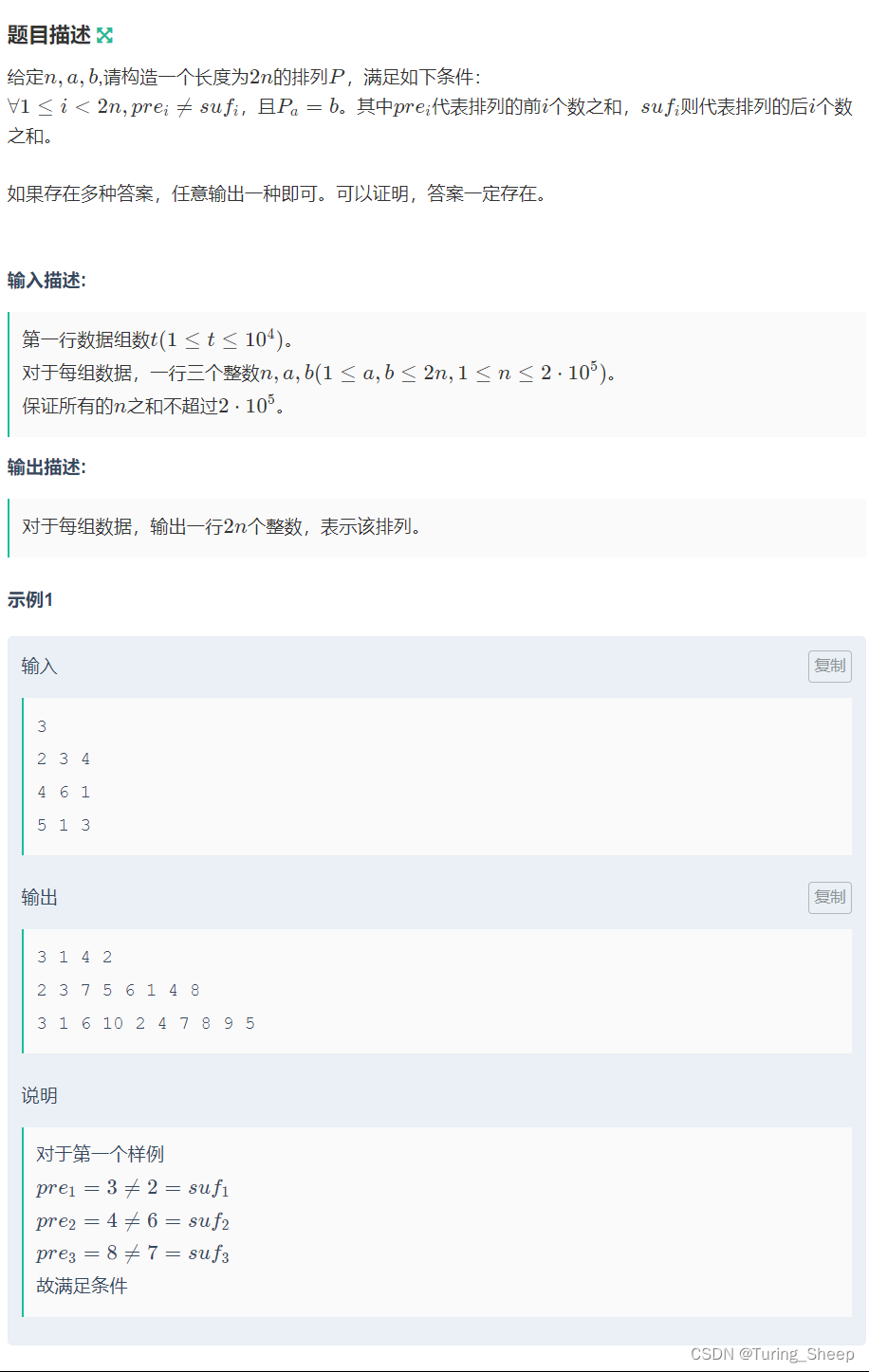
二、分析

我们只需要以中间作为分割点，一侧放比nnn大的数，另一侧放小于等于nnn的数。这样就能保证前缀和与后缀和是不相等的。
到底是那一侧放大于nnn的，那一侧放小于等于nnn的，取决于题目中固定的bbb放在了那一侧。如果bbb小于等于nnn，那么这一侧就放小于等于nnn的，另一侧就放大于nnn的。

接下来我们证明一下这种做法的正确性：

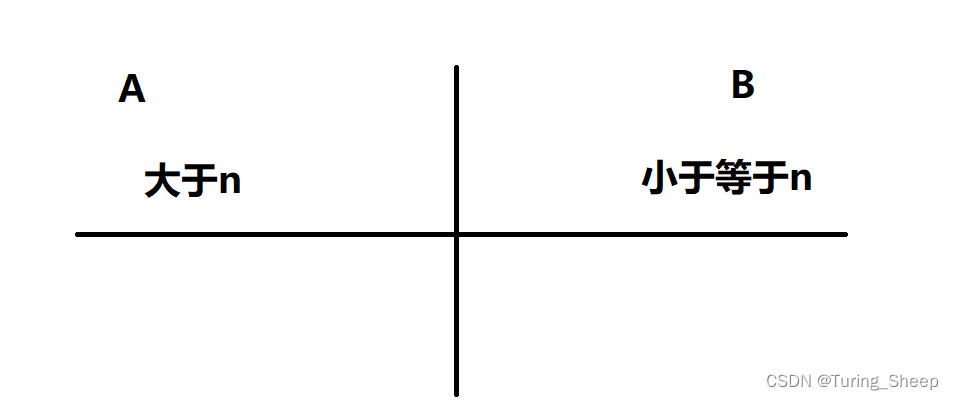
上图就是我们刚刚构造的逻辑，我们从中间将这个数组分开，观察一下，中间线左侧的前缀和是否和中间线右侧的后缀和相等。

因为左侧的数字都大于n，右侧的数字都小于等于n，所以左侧的数字大于右侧的数字，所以左侧的数字构成的前缀和也一定大于右侧数字构成的后缀和。即不存在相等的情况。

接下来，我们再考虑当前缀和与后缀和越过中间线的情况。
这种情况有什么特别的呢？特别之处在于，当我们越过中间线以后，左侧的前缀和开始加上一些小于等于n的数，右侧的后缀和开始加上一些大于等于n的数字，那么在这种情况下是否可能相等呢？

左侧的前缀和等于数组总和减去左侧没有加上的数，右侧的后缀和等于数组总和减去右侧没有加上的数。
因为被减数相同，所以只有在二者没有加上的数字和相同时，前缀和与后缀和才有可能相等。

由于前后缀的元素个数是相等的，所以他们没有加上的数字的个数是相等的。前缀和没有加上的数都是小于等于n的，后缀和没有加上的数都是大于n的。所以后缀和没加上的数一定是大于前缀和没加上的数，因此二者不可能相等。

三、代码

#include
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair pii;
const int N = 1e5 + 10;void solve()
{int n, a, b;cin >> n >> a >> b;vectornums(2 * n);nums[a - 1] = b;if(b > n){if(a > n){int cnt = n + 1;for(int i = n; i < 2 * n; i ++ ){if(i == a - 1)continue;if(cnt != b){nums[i] = cnt ++; }else{cnt ++;nums[i] = cnt ++;}}for(int i = 0; i < n; i ++){nums[i] = i + 1;}}else{int cnt = n + 1;for(int i = 0; i < n; i ++ ){if(i == a - 1)continue;if(cnt != b){nums[i] = cnt ++; }else{cnt ++;nums[i] = cnt ++;}}cnt = 0;for(int i = n; i < 2 * n; i ++){nums[i] = ++ cnt;}}}else{if(a > n){int cnt = 1;for(int i = n; i < 2 * n; i ++ ){if(i == a - 1)continue;if(cnt != b){nums[i] = cnt ++; }else{cnt ++;nums[i] = cnt ++;}}for(int i = 0; i < n; i ++){nums[i] = n + i + 1;}}else{int cnt = 1;for(int i = 0; i < n; i ++ ){if(i == a - 1)continue;if(cnt != b){nums[i] = cnt ++; }else{cnt ++;nums[i] = cnt ++;}}for(int i = n; i < 2 * n; i ++){nums[i] = i + 1;}}}for(auto x : nums){cout << x << " ";}cout << endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;cin >> t;while(t--)solve();
}