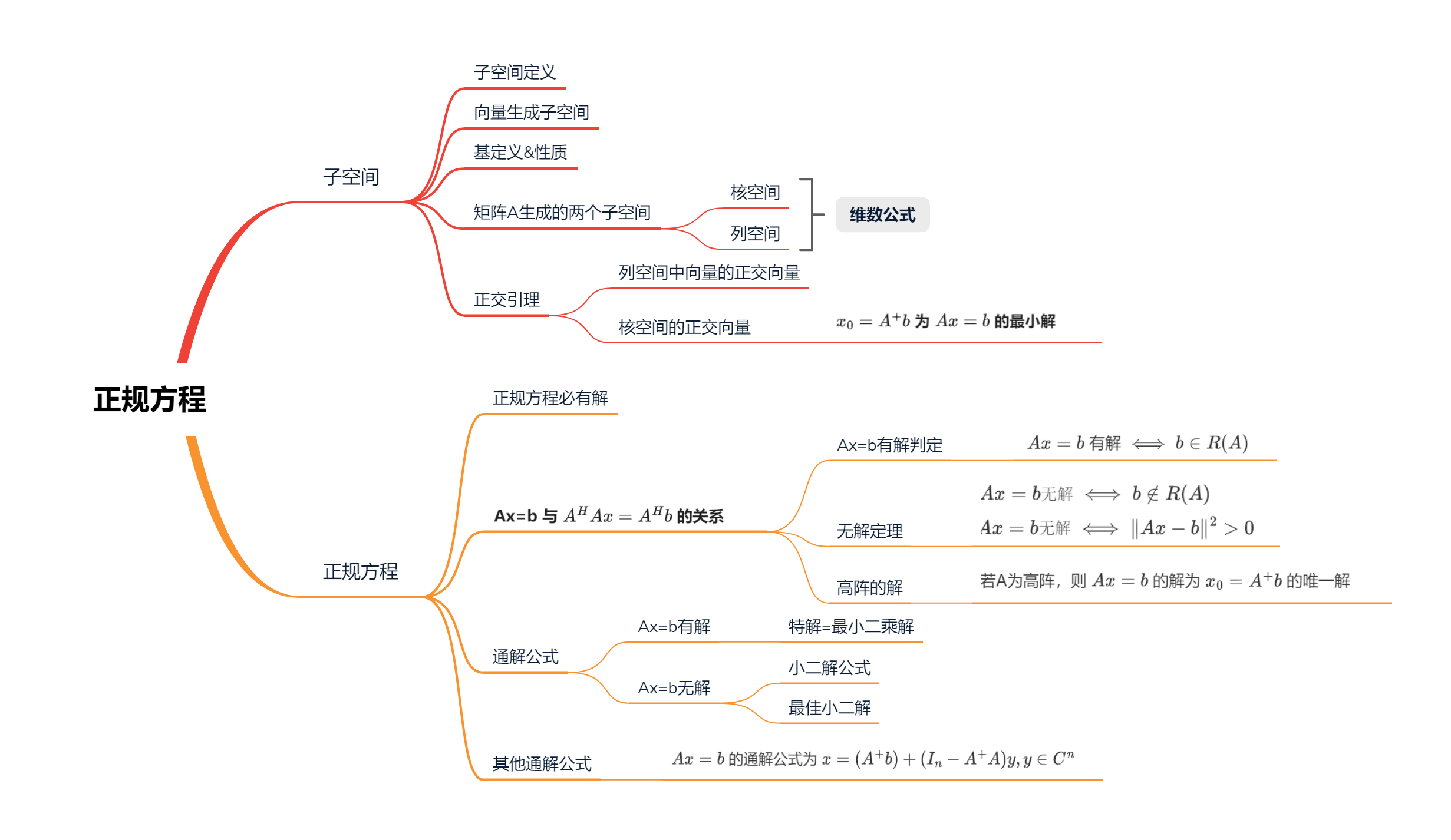
5.2 正规方程

AHAx=AHb为Ax=b的正规方程\begin{aligned} A^HAx=A^Hb为Ax=b的正规方程 \end{aligned} AHAx=AHb为Ax=b的正规方程​

5.2.1 正规方程必有解

正规方程 AHAx=AHbA^HAx=A^HbAHAx=AHb 必有解 ，且特解为 x0=A+bx_0=A^+bx0​=A+b ，使 AHAx0=AHbA^HAx_0=A^HbAHAx0​=AHb

证明
由于AHAA+=(AA+)H=AA+AH(AA+)H=(AA+A)H=AH,令x0=A+b,则AAHx0=AHAA+b=AHb\begin{aligned} &由于A^HAA^+\xlongequal{(AA^+)^H=AA^+}A^H(AA^+)^H=(AA^+A)^H=A^H,\\ &令x_0=A^+b,则AA^Hx_0=A^HAA^+b=A^Hb \end{aligned} ​由于AHAA+(AA+)H=AA+AH(AA+)H=(AA+A)H=AH,令x0​=A+b,则AAHx0​=AHAA+b=AHb​
推论

若矩阵方程 AXD=BAXD=BAXD=B 有解，则有特解 X1=A+BD+X_1=A^+BD^+X1​=A+BD+

5.2.2 Ax=b 与 AHAx=AHbA^HAx=A^HbAHAx=AHb 的关系

1.若Ax=b有解，则AHAx=AHb有解，且两个方程组同解（相容）2.若Ax=b无解，则AHx=AHb仍然有解，且特解为A+b（不相容）1.若Ax=b有解，则 A^HAx=A^Hb有解，且两个方程组同解（相容）\\ 2.若Ax=b无解，则 A^Hx=A^Hb仍然有解，且特解为A^+b（不相容） 1.若Ax=b有解，则AHAx=AHb有解，且两个方程组同解（相容）2.若Ax=b无解，则AHx=AHb仍然有解，且特解为A+b（不相容）

a. Ax=bAx=bAx=b 有解判定

若 Ax=bAx=bAx=b 有解(相容)，则可知 b∈R(A)={y=Ax∣x∈Cn}b\in R(A)=\{y=Ax\vert x\in C^n\}b∈R(A)={y=Ax∣x∈Cn} ，即 Ax=bAx=bAx=b 有解 ⟺\iff⟺ b∈R(A)b\in R(A)b∈R(A)

b. 无解定理

若Ax=b无解(不相容)，则对一切x∈Cn,Ax≠b,即Ax=b无解⟺b∉R(A)若Ax=b无解，则队一切x∈Cn，Ax≠b必有∥Ax−b∥2>0,即Ax=b无解⟺∥Ax−b∥2>0若Ax=b无解(不相容)，则对一切x\in C^n,Ax\neq b,即Ax=b无解\iff b\notin R(A)\\ 若Ax=b无解，则队一切x\in C^n，Ax\neq b必有\Vert Ax-b\Vert^2>0,即 Ax=b无解\iff \Vert Ax-b \Vert^2>0 若Ax=b无解(不相容)，则对一切x∈Cn,Ax​=b,即Ax=b无解⟺b∈/​R(A)若Ax=b无解，则队一切x∈Cn，Ax​=b必有∥Ax−b∥2>0,即Ax=b无解⟺∥Ax−b∥2>0

若x0=A+b使Ax0≠b,则Ax=b无解（不相容）若x_0=A^+b 使Ax_0\neq b,则 Ax=b 无解（不相容） 若x0​=A+b使Ax0​​=b,则Ax=b无解（不相容）

c. 高阵的解

若 A=Am×nA=A_{m\times n}A=Am×n​ 为列满秩阵，则有 N(A)={0⃗}N(A)=\{\vec{0}\}N(A)={0} ，即 AX=0AX=0AX=0 只有零解 X=0⃗X=\vec{0}X=0

若A为高阵，则 Ax=bAx=bAx=b 的解为 x0=A+bx_0=A^+bx0​=A+b 的唯一解

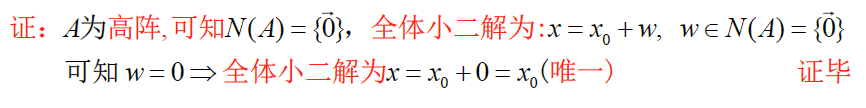
eg

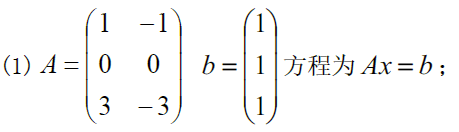
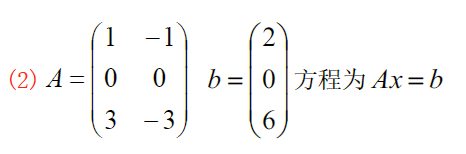
5.2.3 通解公式

a. Ax=bAx=bAx=b 有解情形

设 Ay=0Ay=0Ay=0 基本解为 Y1,Y2,⋯,YkY_1,Y_2,\cdots,Y_kY1​,Y2​,⋯,Yk​ ，则 Ay=0Ay=0Ay=0 有通解，y=t1Y1+t2Y2+⋯+tkYky=t_1Y_1+t_2Y_2+\cdots+t_kY_ky=t1​Y1​+t2​Y2​+⋯+tk​Yk​ ,可写 N(A)={y∣Ay=0}={全体y=t1Y1+t2Y2+⋯+tkYk}N(A)=\{y\vert Ay=0\}=\{全体y=t_1Y_1+t_2Y_2+\cdots+t_kY_k\}N(A)={y∣Ay=0}={全体y=t1​Y1​+t2​Y2​+⋯+tk​Yk​} k=n-r(A)

且 Ay=bAy=bAy=b 通解公式为 x=x0+(t1Y1+t2Y2+⋯+tkYk)=Δx0+y,∀y∈N(A)x=x_0+(t_1Y_1+t_2Y_2+\cdots+t_kY_k)\xlongequal{\Delta}x_0+y,\forall y\in N(A)x=x0​+(t1​Y1​+t2​Y2​+⋯+tk​Yk​)Δx0​+y,∀y∈N(A)

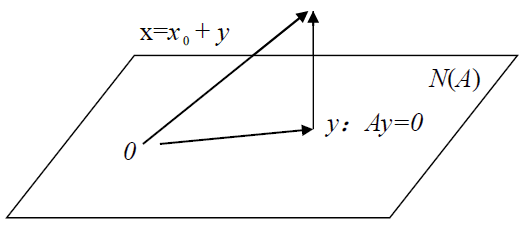
最小二乘解

若 Ax=bAx=bAx=b 有解，则哪个解x的长度平方 $\vert x\vert^2=xHx=\vert x_1\vert^2+\cdots+\vert x_k\vert^2 $ 最小：x0=A+bx_0=A^+bx0​=A+b

eg

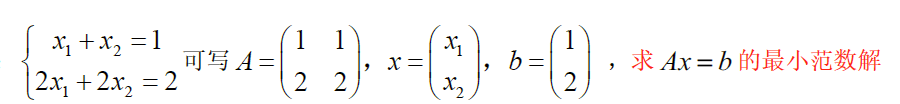
r(A)=r(A∣b)=1，故Ax=b有解x0=A+b=(1122)+b=110(1212)(12)=110(55)=(1212)Ax=0⇒(1122)(x1x2)=0⇒x1+x2=0⇒Ax=0通解x=(1−1)Ax=b的通解公式为X=(1212)+t(1−1)\begin{aligned} &r(A)=r(A\vert b)=1，故Ax=b有解\\ &x_0=A^+b=\left( \begin{matrix} 1&1\\2&2 \end{matrix} \right)^+b=\frac{1}{10}\left( \begin{matrix} 1&2\\1&2 \end{matrix} \right)\left( \begin{matrix} 1\\2 \end{matrix} \right)=\frac{1}{10}\left( \begin{matrix} 5\\5 \end{matrix} \right)=\left( \begin{matrix} \frac{1}{2}\\\frac{1}{2} \end{matrix} \right)\\ &Ax=0\Rightarrow\left( \begin{matrix} 1&1\\2&2 \end{matrix} \right)\left( \begin{matrix} x_1\\x_2 \end{matrix} \right)=0\Rightarrow x_1+x_2=0\Rightarrow Ax=0通解x=\left( \begin{matrix} 1\\-1 \end{matrix} \right)\\ &Ax=b的通解公式为 X=\left( \begin{matrix} \frac{1}{2}\\\frac{1}{2} \end{matrix} \right)+t\left( \begin{matrix} 1\\-1 \end{matrix} \right) \end{aligned} ​r(A)=r(A∣b)=1，故Ax=b有解x0​=A+b=(12​12​)+b=101​(11​22​)(12​)=101​(55​)=(21​21​​)Ax=0⇒(12​12​)(x1​x2​​)=0⇒x1​+x2​=0⇒Ax=0通解x=(1−1​)Ax=b的通解公式为X=(21​21​​)+t(1−1​)​

b. Ax=bA x=bAx=b 无解情形

若 Ax=bAx=bAx=b 无解，则 ∣Ax−b∣2>0\vert Ax-b\vert^2>0∣Ax−b∣2>0 ，对于 x∈Cnx\in C^nx∈Cn ，如何使 ∣Ax−b∣\vert Ax-b\vert∣Ax−b∣ 最小：x0=A+bx_0=A^+bx0​=A+b

若 ∣Ax0−b∣2\vert Ax_0-b\vert ^2∣Ax0​−b∣2 为 ∣Ax−b∣2\vert Ax-b\vert^2∣Ax−b∣2 的最小值，则 x0x_0x0​ 为 Ax−bAx-bAx−b 的一个极小二乘解，即 ∣Ax0−b∣2\vert Ax_0-b\vert^2∣Ax0​−b∣2 为 AXAXAX 与 bbb 的最小平方距离

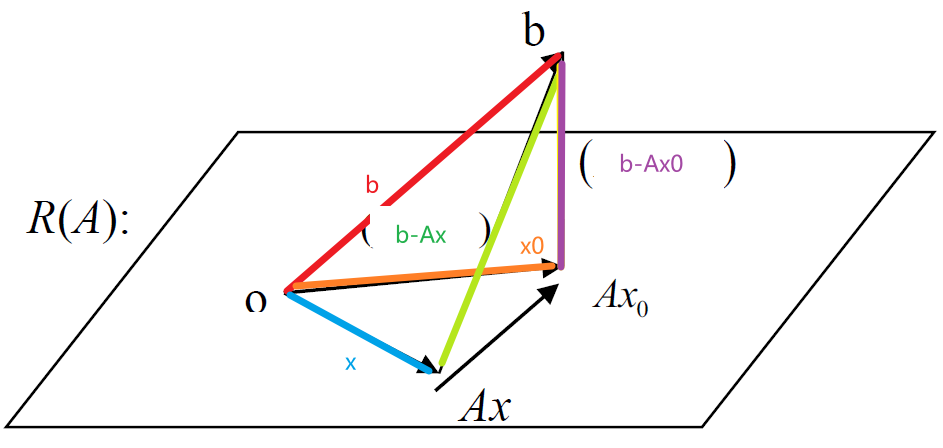
证明
Ax−Ax0=A(x−x0)∈R(A),∴(b−Ax0)⊥A(x−x0)∣Ax−b∣2=勾股定理∣A(x−x0)+A(x0−b)∣2≥∣A(x−x0)∣2+∣A(x0−b)∣2≥∣A(x0−b)∣2当且仅当A(x−x0)=0时，∣Ax0−b∣2=∣A(x0−b)∣2最小\begin{aligned} &Ax-Ax_0=A(x-x_0)\in R(A),\therefore (b-Ax_0)\bot A(x-x_0)\\ &\vert Ax-b\vert^2\xlongequal{勾股定理}\vert A(x-x_0)+A(x_0-b)\vert^2 \ge \vert A(x-x_0)\vert^2 + \vert A(x_0-b)\vert^2\ge \vert A(x_0-b)\vert^2\\ &当且仅当A(x-x_0) =0时， \vert Ax_0-b\vert^2=\vert A(x_0-b)\vert ^2最小 \end{aligned} ​Ax−Ax0​=A(x−x0​)∈R(A),∴(b−Ax0​)⊥A(x−x0​)∣Ax−b∣2勾股定理∣A(x−x0​)+A(x0​−b)∣2≥∣A(x−x0​)∣2+∣A(x0​−b)∣2≥∣A(x0​−b)∣2当且仅当A(x−x0​)=0时，∣Ax0​−b∣2=∣A(x0​−b)∣2最小​

小二解公式

令 x0=A+bx_0=A^+bx0​=A+b ，则 Ax=bAx=bAx=b 的全体小二解为 x=x0+Y,Y∈N(A),AY=0x=x_0+Y,Y\in N(A),AY=0x=x0​+Y,Y∈N(A),AY=0

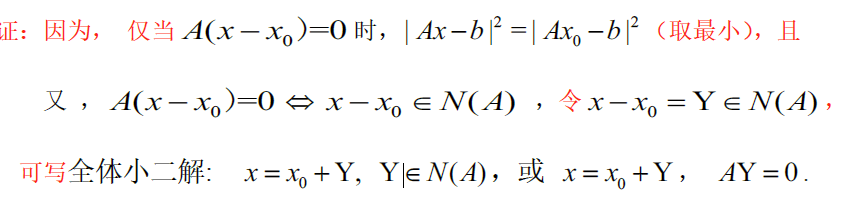
最佳小二解

若 Ax=bAx=bAx=b 无解，则 x0=A+bx_0=A^+bx0​=A+b 为最佳小二解

eg

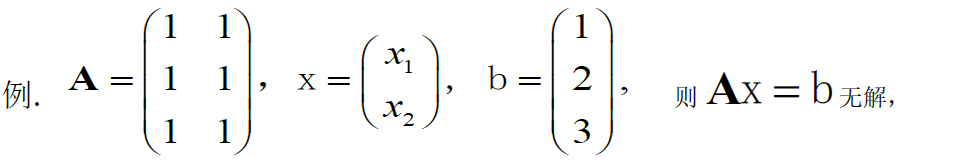
r(A)=1,r(A∣b)=3，故Ax=b无解最佳小二解x0=A+b=16(111111)(123)=(11),令Ay=0,⇒x1+x2=0,即Y=(1−1)全体小二解为X=x0+tY=(11)+t(1−1)\begin{aligned} &r(A)=1,r(A\vert b)=3，故Ax=b无解\\ &最佳小二解x_0=A^+b=\frac{1}{6}\left( \begin{matrix} 1&1&1\\1&1&1 \end{matrix} \right)\left( \begin{matrix} 1\\2\\3 \end{matrix} \right)=\left( \begin{matrix} 1\\1 \end{matrix} \right),令Ay=0,\Rightarrow x_1+x_2=0,即Y=\left( \begin{matrix} 1\\-1 \end{matrix} \right)\\ &全体小二解为X=x_0+tY=\left( \begin{matrix} 1\\1 \end{matrix} \right)+t\left( \begin{matrix} 1\\-1 \end{matrix} \right) \end{aligned} ​r(A)=1,r(A∣b)=3，故Ax=b无解最佳小二解x0​=A+b=61​(11​11​11​)⎝⎛​123​⎠⎞​=(11​),令Ay=0,⇒x1​+x2​=0,即Y=(1−1​)全体小二解为X=x0​+tY=(11​)+t(1−1​)​

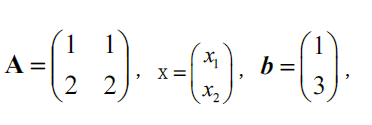
r(A)=1≠r(A∣b)=2,∴Ax=b无解最佳小二解x0=A+b=110(1212)(13)=110(77)设Ay=0⇒(1122)(y1y2)=y1+y2=0⇒齐次方程Ay=0的通解为y=(1−1)∴Ax=b的通解为x=x0+ty=110(77)+t(1−1)\begin{aligned} &r(A)=1\neq r(A\vert b)=2,\therefore Ax=b无解\\ &最佳小二解x_0=A^+b=\frac{1}{10}\left( \begin{matrix} 1&2\\1&2 \end{matrix} \right)\left( \begin{matrix} 1\\3 \end{matrix} \right)=\frac{1}{10}\left( \begin{matrix} 7\\7 \end{matrix} \right)\\ &设Ay=0\Rightarrow \left( \begin{matrix} 1&1\\2&2 \end{matrix} \right)\left( \begin{matrix} y_1\\y_2 \end{matrix} \right)=y_1+y_2=0\Rightarrow 齐次方程Ay=0的通解为 y=\left( \begin{matrix} 1\\-1 \end{matrix} \right)\\ &\therefore Ax=b的通解为 x=x_0+ty=\frac{1}{10}\left( \begin{matrix} 7\\7 \end{matrix} \right)+t\left( \begin{matrix} 1\\-1 \end{matrix} \right) \end{aligned} ​r(A)=1​=r(A∣b)=2,∴Ax=b无解最佳小二解x0​=A+b=101​(11​22​)(13​)=101​(77​)设Ay=0⇒(12​12​)(y1​y2​​)=y1​+y2​=0⇒齐次方程Ay=0的通解为y=(1−1​)∴Ax=b的通解为x=x0​+ty=101​(77​)+t(1−1​)​

5.2.4 其他通解公式

a. Ax=0Ax=0Ax=0 的通解公式

Ax=0的通解为ξ=(In−A+A)y,y∈CnAx=0的通解为 \xi=(I_n-A^+A)y,y\in C^n\\ Ax=0的通解为ξ=(In​−A+A)y,y∈Cn

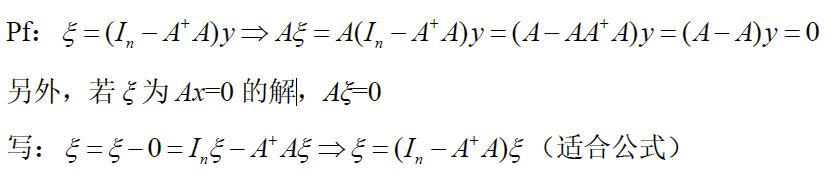
可写核空间公式 N(A)={w=(I−A+A)y∣y∈Cn}N(A)=\{w=(I-A^+A)y\vert y\in C^n\}N(A)={w=(I−A+A)y∣y∈Cn}

b. Ax=bAx=bAx=b 的通解

Ax=bAx=bAx=b 的通解公式为 x=(A+b)+(In−A+A)y,y∈Cnx=(A^+b)+(I_n-A^+A)y,y\in C^nx=(A+b)+(In​−A+A)y,y∈Cn